5

I have understood the definition of group automorphism and have studied various examples for the same. But what is the significance of an automorphism? When we study isomorphisms, we try to investigate how similar is a group to another group. What do we get from establishing isomorphisms from a group to itself?

Ajay Shanmuga Sakthivasan
  • 211
  • We can realise other groups as automorphism groups, e.g., $Aut(Q_8)\cong S_4$, see here. – Dietrich Burde Dec 01 '18 at 12:01
  • You can make rings out of group by taking its automorphism group, Ex, Integer ring is the automorphism ring of $(\mathbb{Z},+)$. – user614287 Dec 01 '18 at 13:01
  • @mathnoob That needs further explanation to be valid. A straightforward reading would suggest you mean to say that the integers are the endomorphism ring of $(\Bbb{Z},+)$, not an "automorphism ring," which is undefined. – jgon Dec 01 '18 at 17:50

2 Answers2

10

An automorphism on a structure describes a symmetry on that structure - a way in which certain elements of the structure play identical roles within the structure.

For example, a graph isomorphism is a bijection between the sets of nodes of two graphs such that $x$ and $y$ are adjacent (have an edge connecting them) if and only if $f(x)$ and $f(y)$ are adjacent. This means that the two graphs are really the same graph (they can be made to look identical if they're drawn in the right way).

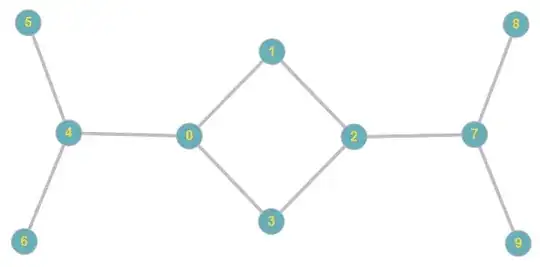
Now look at this graph:

enter image description here

I'm sure you would understand what I meant if I said that the vertices 5, 6, 8 and 9 all "play the same role" in the graph. Vertices 0 and 2 also "play the same role". But vertices 5 and 1 play very different roles, they don't fit into the graph in identical ways (for example, 5 has one neighbor while 1 has two). This is due to the obvious symmetries which exist in this graph, corresponding to the two automorphisms of the graph given by:

  1. $f$ such that $f(5)=6, f(6)=5, f(1)=3, f(3)=1, f(8)=f(9)$, and $f(x)=x$ for all other nodes.

  2. $g$ such that $g(5)=8, g(8)=5, g(4)=7, g(7)=4, g(0)=2,g(2)=0, g(6)=9, g(9)=6$, and $g(x)=x$ for all other nodes.

The fact that 5 and 1 do not play the same role corresponds to the fact that there is no automorphism mapping 5 to 1 or vice-versa.

Jack M
  • 27,819
  • 7
  • 63
  • 129
4

To me the best motivation for studying group automorphisms is their application to semi-direct products. For example, in the classification of groups of order $pq$ for distinct primes $p$ and $q$, you can use the Sylow theorems to show that $G$ is some semi-direct product of $C_p$ and $C_q$. Knowing the structure of $\text{Aut}(C_p)$ is then crucial in proving that in fact there is only one non-Abelian semi-direct product of $C_p$ and $C_q$ up to isomorphism. In general, when trying to classify groups of a given order understanding semi-direct products can be very useful. To do this, we first should understand automorphism groups.

Sean Haight
  • 1,368