Does there exists a rational parametrization of quadratic surfaces? In particular, I want to parametrize hyperboloid of one sheet $\frac{x^2}{b}+\frac{y^2}{4b}-\frac{z^2}{4b}=1$ where $b$ is rational. (https://en.wikipedia.org/wiki/Hyperboloid).
In the above link, it says that plane section of hyperboloid is conic (or lines) and we can parametrize the conics rationally. Will this generate all the rational solutions on my hyperboloid? Is there any good reference on this stuff?
Certainly, this is always possible. One useful tool here is the so-called Weierstrass substitution, $t\mapsto 2\arctan u$. This can then be combined with the usual trigonometric relations
$$\cos^2 t+\sin^2 t=1\; \longrightarrow \left(\frac{1-u^2}{1+u^2}\right)^2+\left(\frac{2u}{1+u^2}\right)^2=1$$
(a.k.a. stereographic projection); and
$$\sec^2 t-\tan^2 t=1\; \longrightarrow \left(\frac{1+u^2}{1-u^2}\right)^2-\left(\frac{2u}{1-u^2}\right)^2=1$$
to build up rational parametrizations for quadric surfaces. (Incidentally, the existence of these rational parametrizations is also why one can use nonuniform rational B-splines (NURBS) to represent quadric surfaces.)
For the specific case of the one sheet hyperboloid
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$
we have the trigonometric parametrization (prove this as an exercise!):
$$\begin{align*} x&=a\cos \theta\sec \lambda\\ y&=b \sin \theta\sec \lambda\\ z&=c\tan \lambda \end{align*}$$
and using the Weierstrass substitution on it yields
$$\begin{align*} x&=a\frac{(1-u^2)(1+v^2)}{(1+u^2)(1-v^2)}\\ y&=b\frac{2 u (1+v^2)}{(1+u^2)(1-v^2)}\\ z&=c\frac{2 v}{1-v^2} \end{align*}$$
Similar constructions can be used for other quadrics.
In order to obtain your parametrization I would first show that one-sheet hyperboloid is a rational variety, which means that it is birationally equivalent to $\mathbb{P}^2$. Then in the 2nd step we modify the rational map $\psi:\mathbb{P}^2\dashrightarrow\mathbf{V}(P_{h})$ to become our desired parametrization.
Homogenize the polynomial function. Note that you'll be obtaining a projective variety in $\mathbb{P}^3$ represented by the zero of the following polynomial:
$$P_{h} := -{\frac {4\,{w}^{2}b-4\,{x}^{2}-{y}^{2}+{z}^{2}}{4\,b}}$$
Then consider the map
$$\phi: U\subset \mathbf{V}\left(P_{h}\right) \dashrightarrow \mathbb{P}^2\\ (x:y:z:w) \mapsto (x:y-z:w) $$ where $U = \mathbf{V}(P_{h})\setminus\{\left( 0:1:1:0 \right)\}$. This gives a rational map from our quadric to $\mathbb{P}^2$ (geometrically this is very similar to the idea of parametrization of a circle using a pencil of lines).
Now, by naming $$ X = x\\ Y = y-z\\ W = w $$ and solving the above equations for $x$, $y$ and $w$ and substituting them in $P_h$ we obtain $z$. Consequently, this gives the rational map:
$$ \psi : U^{\prime}\subset \mathbb{P}^2 \dashrightarrow \mathbf{V}\left(P_{h}\right)\\ (X:Y:W) \mapsto \left( X : -{\frac {4\,{X}^{2}-{Y}^{2}-4\,W^2\,b}{2\,Y}}:-{\frac {4\,{X}^{2}+{Y}^{2}-4\,W^2\,b}{2\,Y}}:W\right) $$ where $U^{\prime} = \mathbb{P}^2\setminus\mathbf{V}(Y)$. The rest is easy to check that $\psi$ and $\phi$ give the birational equivalency of $\mathbf{V}(P_{h})$ and $\mathbb{P}^2$. Finally a good way to obtain our rational parametrization that we are looking for is to put $W = 1$. Hence the final parametrization could be written as:
$$ x = X\\ y = -{\frac {4\,{X}^{2}-{Y}^{2}-4\,b}{2\,Y}}\\ z = -{\frac {4\,{X}^{2}+{Y}^{2}-4\,b}{2\,Y}} $$
Note that for such a parametrization one is allowed to take all but the $Y = 0$.
Finally, it could be helpful to take a look at the visual result of our parametrization. Here I provided the picture for $b = 1/2$. The blue hologram of hyperboloid is created using its implicit function while the "more accurate" portions of it are produced using our rational parametrization for $X \in [-2,2]$ and $Y \in [-18, -0.8] \cup [0.8, 18]$.
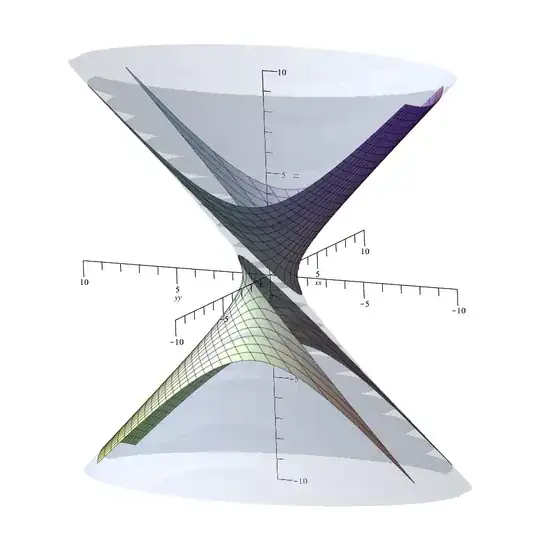
(for a non-rational parameterization of one-sheet hyperboloids see Hyperboloid-Wikipedia).
