2

Curiosity

Let $\mathscr{C}$ be a circle of radius $r$, centered at the origin.

Assign point $O$ the cartesian coordinate $(0,0).$

Let $k$ be a fixed element in $(0,r).$

Set points A and B to have cartesian coordinates $(0,k)$ and $(0,-k)$ respectively.

Choose point C at random on $\mathscr{C}.\;$ Then $\;\left|\;\overline{OC}\;\right|^2 = r^2.$

The end of this query gives an Algebraic Demonstration that
regardless of the point $C$ chosen, $\;\left|\;\overline{AC}\;\right|^2 + \left|\;\overline{BC}\;\right|^2 = 2(r^2 + k^2).$

Questions

Question 1 below added, per Blue's suggestion.

  1. see this query's Background section (the next section). My underlying desire is to find a non-algebraic way of predicting that
    given $\;z_1,z_2 \in \mathbb{C}\;$ the Locus of $\;\{z\; :\; |z-z_1|^2 + |z-z_2|^2 \;=\;$ a constant$\}\;$ will be a circle. I have accepted Blue's answer, re Appollonious' (triangle-oriented) theorem, which does facilitate the prediction, though the logic is convoluted. I would welcome a separate circle-oriented geometry theorem that more directly facilitates the prediction.

The remaining questions in this section are now somewhat redundant, but are left in as a reference to how I originally posed my questions.

  1. Can this result be demonstrated geometrically, without resorting to algebra?

  2. Does this result have a (theorem) name?

  3. Is there a free online geometry resource (e.g. pdf) that includes this result?

Background

In "An Introduction to Complex Function Theory", Bruce Palka, 1991, problem 4.6.vii, p.26 specifies:
geometrically describe $\;\{z\;:\;\left|z-i\right|^2 + \left|z+i\right|^2 = 4\}.\;$
After determining that the Locus was a circle of radius 1, centered at the origin, I realized that
if the right hand side $\; = R \;: \;R>2\;$ then the Locus is a circle of radius $\;\sqrt{(R-2)/2}.$
My (brief) subsequent online research found no mention of this curious result.

Algebraic Demonstration

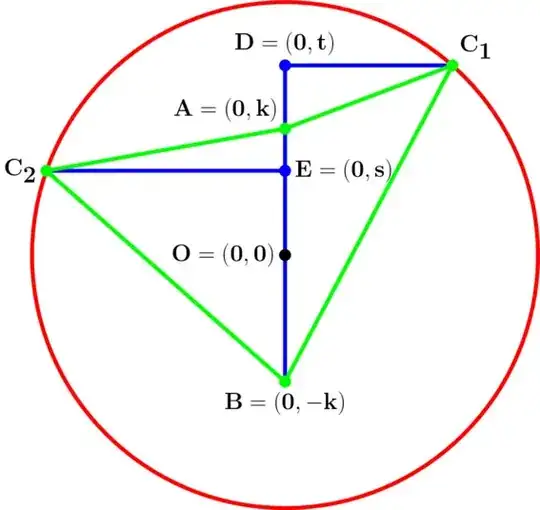
In the diagram at the end of this query, $\;\mathscr{C}, r, k,\;$ point $A$ and point $B$ are as described in the Curiousity section, at the start of this query.

Randomly choose $t$ in $\;(k, r)\;$ and assign point $D$ the cartesian coordinates $(0,t).$

Let point $C_1$ represent the right-hand-side intersection of $\;\mathscr{C}\;$ with the line $\;y=t.$

Similarly, randomly choose $s$ in $\;(0,k),\;$ and assign point $E$ the cartesian coordinate $\;(0,s).$

Similarly, let point $C_2$ represent the left-hand-side intersection of $\;\mathscr{C}\;$ with the line $\;y=s.$

$\left|\;\overline{DC_1}\;\right|^2 \;= \;r^2 - t^2.$
$\left|\;\overline{AC_1}\;\right|^2 \;= \;(t-k)^2 + \left|\;\overline{DC_1}\;\right|^2.$
$\left|\;\overline{BC_1}\;\right|^2 \;= \;(t+k)^2 + \left|\;\overline{DC_1}\;\right|^2.$
$\left|\;\overline{AC_1}\;\right|^2 + \left|\;\overline{BC_1}\;\right|^2 \;= \;2(t^2 + k^2) \;+ \;2(r^2 - t^2) \;= \;2(r^2 + k^2).$

$\left|\;\overline{EC_2}\;\right|^2 \;= \;r^2 - s^2.$
$\left|\;\overline{AC_2}\;\right|^2 \;= \;(k-s)^2 + \left|\;\overline{EC_2}\;\right|^2.$
$\left|\;\overline{BC_2}\;\right|^2 \;= \;(k+s)^2 + \left|\;\overline{EC_2}\;\right|^2.$
$\left|\;\overline{AC_2}\;\right|^2 + \left|\;\overline{BC_2}\;\right|^2 \;= \;2(k^2 + s^2) \;+ \;2(r^2 - s^2) \;= \;2(r^2 + k^2).$

enter image description here

user2661923
  • 35,619
  • 3
  • 17
  • 39
  • This can be considered simple application of the Law of Cosines and the fact that supplementary angles have negative cosines. $$\begin{align}0 &= 2kr (\cos\angle COA+\cos\angle COB) \ &= (|AC|^2-k^2-r^2)+(|BC|^2-k^2-r^2) \ &=|AC|^2+|BC|^2-2(k^2+r^2)\end{align}$$ (I don't know if you'd consider this too "algebraic".) I'm not aware of any name for this result; it doesn't seem to need one. – Blue Dec 19 '18 at 04:27
  • By the way, this answer of mine gives a geometric derivation of the Law of Cosines. – Blue Dec 19 '18 at 04:44
  • @Blue slick...(but still algebraic). I am actually surprised that my result isn't less obscure. – user2661923 Dec 19 '18 at 05:18
  • I'll note that the result has nothing to do with a circle; rather, it's simply a triangle relation. In particular, it relates the length of a median to other segments in a triangle. In that regard, it's a special case of Stewart's Theorem. (Ah! As the Wikipedia entry notes, the median case does have a name: Apollonius's Theorem.) – Blue Dec 19 '18 at 05:34

1 Answers1

1

Here's an alternative (but still very "algebraic") derivation that leverages Thales' theorem (the angle inscribed in a semicircle is right):

enter image description here

$$\begin{align} a^2+b^2 &= \left(m^2+p^2\right)+\left(n^2+q^2\right) \\ &=\left(m^2+n^2\right)+\left(p^2+q^2\right) \\ &=\left(r+k\right)^2+\left(r-k\right)^2 \\ &=2\left(r^2+k^2\right) \end{align}$$

This result, which relates the length of a median to other segments in $\triangle ABC$, is Apollonius's Theorem. It's a special case of Stewart's Theorem for the length of an arbitrary cevian.

Blue
  • 75,673
  • unfortunately, I have to accept your answer as on-point. However, examine my question from the point of view of background. The idea is that given $;z_1, z_2 \in\mathbb{C};$, it is desired to predict in advance (without algebra) that the Locus of $;{z;:|z-z_1|^2 + |z-z_2|^2 = ;$a constant$};$ will be a circle. It takes some convoluted logic to use Appollonius' theorem to reach that conclusion. – user2661923 Dec 19 '18 at 06:43
  • You don't "have to" accept any answer that fails to satisfy you, so feel free to un-accept and encourage others to answer. (One should usually allow a bit of time before accepting, anyway.) That said, you could/should make your desire clearer by asking up-front: "How might we anticipate that $|AC|^2+|BC|^2=\text{constant}$ represents a circle?" – Blue Dec 19 '18 at 07:00
  • Good pt, re clarifying my desire; it never occurred to me that an on-point geometric theorem would exist that didn't easily fulfill my underlying desire. Re accept'g your answer, I feel compelled to for two reasons: (1) Your answer is directly on-point and can fulfill my underlying desire, though convoluted logic is involved. (2) Given the existence of Appollonius' (triangle-oriented) theorem, I strongly suspect that there will not be a separate circle-oriented geometry theorem that one might use. Assuming that my suspicion is correct, then your answer is the best I'll get. – user2661923 Dec 19 '18 at 07:20
  • As to the logic being convoluted ... I don't think it is, necessarily. Symmetry requires that the center of the circle be the midpoint ($O$) of $AB$, so, "all we need" is a relation among $|AC|$, $|BC|$, $|OC|$, and, presumably, $|AB|$ (or half thereof). Stewart/Apollonius gives that relation, wherein the constancy of $|AC|^2+|BC|^2$ (and $|AB|$) immediately implies the constancy of $|OC|$. Done. That said, I'm actually inclined to believe that there's a more-satisfying diagrammatic demonstration of this fact. – Blue Dec 19 '18 at 07:32
  • 1
    I edited my query re your suggestion about clarifying my desire. I agree with the logic of your latest comment. My use of the adjective convoluted merely signifies that even if I had been aware of Appollonius' (triangle oriented) theorem, I could have easily overlooked that it can be used to show that the Locus is a circle. Further, since the Locus is a circle, my initial intuition is that some property of circles must be involved. This intuition is similar to the last sentence in your latest comment. – user2661923 Dec 19 '18 at 07:48