I am not completely sure, but the Moiré pattern on photo's of my screen looks suspiciously like a contour plot of z = xy. I couldn't find any reference or similar question. Is there a fundamental reason for this, or does it seem to be merely a coincidence?
Moiré pattern on my screen:
Contour plot of z = xy:
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$ in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
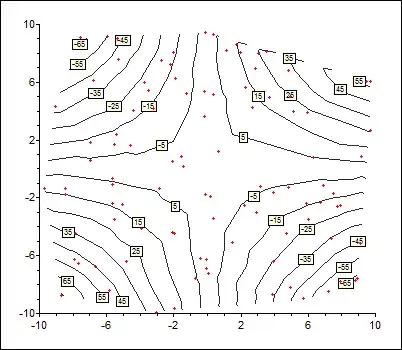
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook. The Moire pattern image with $t=-9/60$ is this:
You can see the resemblance to the top right quarter of the screen shot.
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.
Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{\circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
