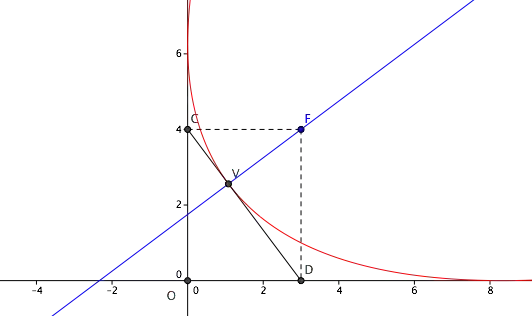
The area of the triangle formed by the coordinate axes and tangent at vertex to the parabola whose focus is $(3,4)$ and tangents at $x=0$ and $y=0$ is?
I know how to do this, assume an equation for parabola with axis as $y=4/3 x$ and do all the procedure. But, this isn't how it is really to be solved. There's a sleek way which I cannot find.