How do Peano Axioms imply "nextness" with the successor?

Question

Going with this explanation of Peano's Axioms, I cannot understand how/where the successor function is definitively stated to be the very next number in the case of natural numbers. In this treatment, it says

The successor of $x$ is sometimes denoted $S⁢x$ instead of $x′$. We then have $1=S⁢0$, $2=S⁢1=S⁢S⁢0$, and so on.

Again, I don't see from the axioms how very next is guaranteed. Neither further on when addition is defined "based on the axioms." It seems a successor function could map "nextness" in many ways, e.g. $Sx$ could be $x+56$, or whatever as long as $Sx$ was something "further up the natural number line." So yes, I know I'm missing something here. . . .

Update

I finally returned to this issue after stumbling across some other sources. Basically, the whole issue of $S$ "jumping around" and not being a strict "next one up the number chain" can be attacked from exposing and forbidding "loop" situations.

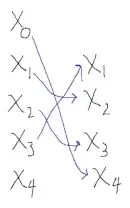
By allowing a successor with $x_3$ circling back to $x_1$, we have with such an $S$ created a "fixed-point" for $S$

$$S(S(S(x_1))) = x_1$$

which is not allowed by the injectivity axiom. See this discussion, which demonstrates a $S(x_k) = x_k$ situation. My example is the same situation, only two extra mappings.

Still, the proof in the proofwiki relies on a hard contradiction backed up by the Peano Induction axiom -- which leaves me a bit pale. Does any sort of $S$ definition with any "fixed point"/loop truly force -- with the induction and injectivity axioms -- "very next one?" Intuitively I can see that any "doubling back" makes for a fixed-point, but....

Answer 1

You're right, it's not obvious. There are a number of interlocking issues.

First let's consider the situation you suggested, where $S(n) = n+57$. We have a couple of choices here. One is to say that the natural numbers are $0, 57, 114, 171, \ldots$, and nothing else is a natural number. Thhis works, but what we get is identical to the regular natural numbers, with different names for the numbers. This system still has $1,2,$ etc., but we are calling them $57, 114$, etc.

Now suppose instead we say that $S(n)=n+57$ and $2, 3,$ etc. are still considered natural numbers. But this fails to satisfy the Peano axioms, specifically the axiom of induction. For suppose $P(n)$ is the statement “$n$ is a multiple of 57”. Certainly $P(0)$ is true, and we can show that if $P(n)$ is true then so is $P(S(n))$. The axiom of induction then says that $P$ is true for all natural numbers. But it's not true for $2$, which contradicts the axiom.

Now let's suppose that it's only $S(0) =57$ and the other numbers have their usual successors. This time the axiom that is violated is the one that says that different numbers have different successors. We have $S(0)=S(56)$ but $0≠56$. We can patch this up by deleting $56$. (Or, equivalently, by agreeing that $56$ is not a natural number.) But now the axiom is violated that says that every number has a successor: what's the successor of $55$?

You can try to patch this up too, but you'll get into trouble some other way. You should think about it and see what happens.

Now let's go the other way: every number has its usual successor, but there's also a natural number $\beta$ between $3$ and $4$. But what is $S(\beta)$? No matter what you try, something breaks.

Does that help?

Answer 2

If you just restrict yourself to the first axioms listed on that page, then indeed you could say that the expressions $0,S(0), S(S(0)), ...$ denote $0,2,1,4,3,6,5,....$ respectively. That would still satisfy the axioms. But you would still have a structure that is isomorphic to the natural numbers.

Also, if you define:

$$\forall x \forall y (x < y \leftrightarrow (y=S(x) \lor \exists z (y = S(z) \land x < z))$$

(which I would think captures the notion of $<$),

then using only those very first axioms, you can prove that:

$$\forall x \neg \exists y (x < y \land y < S(x))$$

i.e. that there is no number between any number and its successor ... and thus that the successor indeed gives you the very next number.

Finally, if you use the addition and multiplication axioms stated later on on that website, then you can prove some results that are certainly very suggestive of $S(0)$ working in a way consistent with our concept of the number $1$.

For example, it follows from the Peano Axioms that $$\forall x ( x · S(0) = x)$$ .... which would make sense if $S(0)$ would take the role we normally reserve for $1$ rather than, say, $56$

Likewise, you can prove from the Peano Axioms that $$\forall x ( x · S(S(0))= x + x)$$ ... again, that would square with the way we think about numbers if $S(S(0))$ is seen as $2$, rather than $117$.

Answer 3

From a formal point of view, PA is written with very few symbols. We are not given the natural numbers or the successor function except as they are defined by the axioms. We are told that there is an element called $0$ and there is a function called $S$ that can be applied to any element of the universe. This is enough to tell us that there is an element that is $SS0$. $2$ is not part of the language but it makes things easier to read and write if we define $2$ to represent $SS0$. We could as well give $SS0$ a name like John, but we choose $2$ because it behaves as the $2$ we learned about in grade school. We can prove from the axioms that $SS0+SS0=SSSS0$, which we would write informally as $2+2=4$.

The author of the axioms can write that he is thinking about $S$ as the successor function, but that is not part of the formal development. From the first two axioms we can show in the metatheory that the universe is infinite, but that is not a conclusion of PA.

Answer 4

I recently really struggled with the same question while studying Peano axioms, but finally, I think I got it. I will mostly repeat what a number of answers and comments said, but I think you still might be missing the idea behind them. It's counterintuitive, so it's hard to change the perspective once you are stuck in the wrong one.

The main point is that natural numbers are not ordered in any way until you define the successor function.

There is no inherent order in the set before you define $S(x)$, so it's misleading to prescribe its elements labels like 55, 56, etc. $S(x)$ can be defined absolutely arbitrary as long as it satisfies the axioms. Only after you defined $S(x)$ do the terms like 55 and 56 make sense. As @Ross Millikan wrote in his comment

We have defined 56 to be …0 with 56 's

So you can't say that

could be +56

because as @Sort of Damocles wrote

The number 56 doesn't exist except that it's the name we give the successor to the number which we have previously named 55

Peano axioms build what we call natural numbers, not merely are built on top of them.

As @Ross Millikan wrote in his answer

2 is not part of the language but it makes things easier to read and write if we define 2 to represent 0. We could as well give 0 a name like John, but we choose 2 because it behaves as the 2 we learned about in grade school.

This means that labels 2, 55, 56, etc are needed only for convenience: 56 is much shorter to write than $SSS...S(0)$ with 56 $S$'s

Answer 5

First, I am not alone in asking this question of "nextness." The following is from the Wikipedia treatment, Peano Axioms:

However, considering the notion of natural numbers as being defined by these axioms, axioms 1, 6, 7, 8 do not imply that the successor function generates all the natural numbers different from 0. Put differently, they do not guarantee that every natural number other than zero must succeed some other natural number.

...which goes on to use the often included axiom of induction to rework the successor function into implying nextness as always "one more." But then the article describes addition as defined recursively by two phantom Peanos:

\begin{align} a + 0 & = a \\ a + S(b) & = S(a + b) \end{align}

If the second expression is considered an axiom, then yes, $S$ would have to be consistently a "one more" successor. That is, there cannot be an $S(b) + a$ that is different from an $S(c)$ where $c = a+b$. However, these addition axioms are not really original to the PAs.

We might fall back on insisting that a successor function cannot from one application to the next behave differently, i.e., (allow me to switch successor notation) $m \succ m'$ implying $m'-m \geq 1$, and then $n \succ n'$ yielding $(n'-n) \neq (m'-m)$ is a violation of the spirit of the successor function and its brother induction.

It is true that $m=n \iff m'=n'$ implies uniqueness of the successor function only in the sense of injection (as pointed out in a comment by Somos). We might say a successor function must be an injective function producing distinct results, e.g., $n'$ is distinct from the successors which produced $1,...,n$, but I'm still doubtful this implies "one more," i.e., $n'$ to $n''$ proceeds one "very next thing" in a strict order at a time.

However, we might be rescued by Kleene's (Introduction to Metamathematics; p.20) example where he leverages the PA that $x' \neq 0$, or, $0$ is not the successor to any natural number. We might set up a contradiction: $$0''''=0''$$ but this would be true only if $$0'''=0'$$ Applying this logic again, $$0'''=0'$$ only if $$0''=0$$ So yes, this is a contradiction; hence, we have butted up against the lower boundary of the successor concept, which, therefore, implies a successor being greater than since we can run any successor-based induction of $\mathbb{N}$ backwards to $0$. Ironically, this is a sort of reverse-induction to prove that the Peano successor is consistently "one more" demanding some sort of $\mathbb{N}$-like order.

All in all, I'm still stuck on this....