2

All of the triangles in the diagram below are similar to isosceles triangle $ABC$, in which $AB=AC$. Each of the 7 smallest triangles has area 1, and $\triangle ABC$ has area 40. What is the area of trapezoid $DBCE$?

enter image description here

Well I approached this problem by trying to find similar triangle ratios. Let the small triangle base be $x$. Then $DE=4x$. That's all I got lol. I couldn't find any other ratios or side lengths. Then, I manually drew triangles composing $\triangle ADE$. This gave me 16 triangles that make up $\triangle ADE$. So thus, $\triangle ADE$ has an area of 16, and trapezoid $BDEC$ has an area of $40-16=\boxed{24}$. Although this is correct, my method of solving comes at a great risk. Is there any better method of solving this question?

Also, if you are nice, could you please also help me on this($N$'s base-5 and base-6 representations, treated as base-10, yield sum $S$. For which $N$ are $S$'s rightmost two digits the same as $2N$'s?) question?

Thanks!

Max0815

Max0815
  • 3,505
  • 1
    ADE is similar to each of the small triangles. The base is 4 times the size.

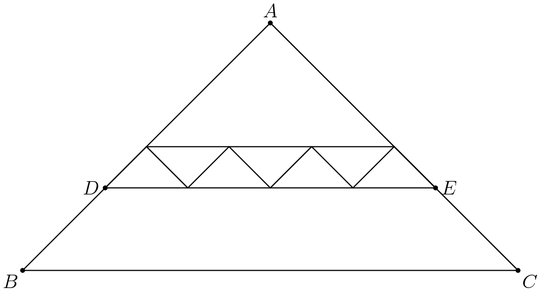
    The area is $4^2$ times as large.

     – Doug M Feb 07 '19 at 00:38

1 Answers1

4

The uppermost triangle has base three times larger than one of the smallest triangles, so its area is nine times larger. That means the area you're looking for is $40-9\times1-7\times1=24$.