Step 1. Substituting $x = 2\sin(\theta/2)$ and noting that
\begin{align*}
\arcsin(x/2)\log(x)
&= (\theta/2) \log(2\sin(\theta/2)) \\
&= \frac{1}{i} \log(e^{i\theta/2}) \log\bigl(i(e^{-i\theta/2} - e^{i\theta/2})\bigr) \\
&= \frac{1}{2}\operatorname{Im}\left[ \log^2\bigl(i(1 - e^{i\theta})\bigr) \right]
\end{align*}
for $0 < \theta < \pi$, the integral is recast as
\begin{align*}
I
&= \frac{1}{2} \int_{0}^{\frac{\pi}{3}} \frac{\sin\theta}{1-2\cos\theta} \operatorname{Im}\left[ \log^2 \left( i(1 - e^{i\theta}) \right) \right] \, \mathrm{d}\theta.
\end{align*}
Here, $\log(\cdot)$ is the principal logarithm. To utilize this, for $0<\epsilon<\frac{\pi}{3}$, we introduce the following auxiliary integral
$$ J_{\epsilon} = \frac{1}{2} \int_{0}^{\frac{\pi}{3}-\epsilon} \frac{\sin\theta}{1-2\cos\theta} \left( \log (1 - e^{i\theta}) + \frac{i\pi}{2} \right)^2 \, \mathrm{d}\theta. $$
$J_{\epsilon}$ is related to $I$ by the relation $I = \lim_{\epsilon \to 0^+}\operatorname{Im}(J_{\epsilon})$.
Step 2. Unfortunately, $J_{\epsilon}$ diverges as $\epsilon \to 0^+$ since its real part does. The key idea in the next step is to decompose $J_{\epsilon}$ that allows to separate the diverging real part from $J_{\epsilon}$.
Consider the curve $\gamma_{\varepsilon}$ in $\mathbb{C}$ which is defined by $\gamma_{\varepsilon}(\theta) = 1 - e^{i\theta}$ for $0 \leq \theta \leq \frac{\pi}{3}-\epsilon$, and substitute $z = \gamma_{\varepsilon}(\theta)$. Then
\begin{align*}
J_{\epsilon}
&= \frac{1}{2} \int_{\gamma_{\epsilon}} \frac{\frac{1}{2i}\bigl((1-z) - \frac{1}{1-z}\bigr)}{1-\bigl((1-z) + \frac{1}{1-z}\bigr)} \left(\log z + \frac{i\pi}{2} \right)^2 \, \frac{\mathrm{d}z}{i(z-1)} \\
&= \frac{1}{4} \int_{\gamma_{\varepsilon}} \left( \frac{3z^2}{z^3+1} - \frac{2z}{z^2-1} \right) \left(\log z + \frac{i\pi}{2} \right)^2 \, \mathrm{d}z \\
&= A_{\epsilon} - B_{\epsilon},
\end{align*}
where $A_{\epsilon}$ and $B_{\epsilon}$ are defined by
$$ A_{\epsilon} = \frac{1}{4} \int_{\gamma_{\varepsilon}} \frac{3z^2}{z^3+1} \left(\log z + \frac{i\pi}{2} \right)^2 \, \mathrm{d}z
\quad\text{and}\quad
B_{\epsilon} = \frac{1}{4} \int_{\gamma_{\varepsilon}} \frac{2z}{z^2-1} \left(\log z + \frac{i\pi}{2} \right)^2 \, \mathrm{d}z. $$
To further simplify these integrals, we observe that
$$ \log z = \frac{1}{2}\log(z^2) = \frac{1}{3}\log (-z^3) - \frac{i\pi}{3} \qquad \text{for } z \in \gamma_{\epsilon}. $$
Here, the last step is a consequence of the branch cut of $\log(\cdot)$ together with the fact that the contours corresponding to $\gamma_{\varepsilon}$, $\gamma_{\varepsilon}^2$, and $-\gamma_{\varepsilon}^3$ are as follows:
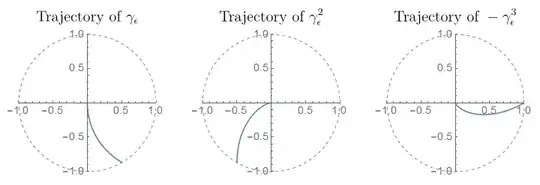
So, by applying further substitutions $-z^3 \mapsto z$ and $z^2 \mapsto z$ to $A_{\epsilon}$ and $B_{\epsilon}$, respectively, we get
\begin{align*}
A_{\epsilon} &= \frac{1}{4} \int_{-\gamma_{\epsilon}^3} \frac{1}{z-1} \left( \frac{1}{3}\log z + \frac{i\pi}{6} \right)^2 \, \mathrm{d}z, \\
B_{\epsilon} &= \frac{1}{4} \int_{\gamma_{\epsilon}^2} \frac{1}{z-1} \left( \frac{1}{2}\log z + \frac{i\pi}{2} \right)^2 \, \mathrm{d}z.
\end{align*}
Step 3. For $A_{\varepsilon}$, the integrand has a simple pole at $z = 1$. Moreover, the terminal point of $-\gamma_{\epsilon}^3$ has an asymptotic formula of the form
$$ -(1-e^{i(\pi/3 - \epsilon)})^3
= 1 - 3e^{i\pi/6}\epsilon + \mathcal{O}(\epsilon^2)
\qquad \text{as $\epsilon \to 0^+$.} $$
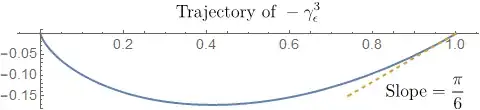
So by replacing $-\gamma_{\epsilon}^3$ by the union of
- $z = x$ for $0 \leq x \leq 1-3\epsilon$, which is the line segment from $0$ to $1-3\epsilon$;
- $z = 1 - 3\epsilon e^{i\theta}$ for $0 \leq \theta \leq \frac{\pi}{6}$, which is the circular arc from $1-3\epsilon$ to $1-3\epsilon e^{i\pi/6}$;
- the line segment from $1-3\epsilon e^{i\pi/6}$ to the terminal point of $-\gamma_{\epsilon}^3$;
it follows that
\begin{align*}
&A_{\epsilon} \\
&= \frac{1}{4} \int_{0}^{1-3\epsilon} \frac{1}{x-1} \left( \frac{1}{3}\log x + \frac{i\pi}{6} \right)^2 \, \mathrm{d}x
+ \frac{i}{4} \int_{0}^{\frac{\pi}{6}} \left( \frac{1}{3}\log(1 - 3\epsilon e^{i\varphi}) + \frac{i\pi}{6} \right)^2 \, \mathrm{d}\varphi
+ \mathcal{O}(\epsilon) \\
&= \frac{i\pi}{36} \int_{0}^{1-3\epsilon} \frac{\log x}{x-1} \, \mathrm{d}x
+ \frac{i}{4} \cdot \frac{\pi}{6} \left( \frac{i\pi}{6} \right)^2
+ \text{[some real number]}
+ \mathcal{O}(\epsilon).
\end{align*}
As $\epsilon \to 0^+$, its imaginary part converges to
$$
\lim_{\epsilon \to 0^+} \operatorname{Im} (A_{\epsilon})
= \frac{\pi}{36} \int_{0}^{1} \frac{\log x}{x-1} \, \mathrm{d}x - \frac{\pi^3}{864}
= \frac{\pi^3}{288}.
$$
Step 4. For $B_{\epsilon}$, its limit is simply $B_0$. So,
$$ \lim_{\epsilon \to 0^+} B_{\epsilon}
= B_0
= \frac{1}{4} \int_{0}^{e^{-2\pi i/3}} \frac{1}{z-1} \left( \frac{1}{2}\log z + \frac{i\pi}{2} \right)^2 \, \mathrm{d}z $$
Performing integration by parts twice, we end up with
$$ \lim_{\epsilon \to 0^+} B_{\epsilon}
= -\frac{\pi^2}{144}\log\bigl(1 - e^{-2\pi i/3} \bigr) + \frac{i\pi}{24} \operatorname{Li}_2\bigl( e^{-2\pi i/3} \bigr) - \frac{1}{8} \operatorname{Li}_3\bigl( e^{-2\pi i/3} \bigr)$$
Although the exact value of $\operatorname{Li}_2\left( e^{-2\pi i/3} \right)$ and $\operatorname{Li}_3\left( e^{-2\pi i/3} \right)$ are not known, it only suffices to know the values of $\operatorname{Re}\left[ \operatorname{Li}_2\left( e^{-2\pi i/3} \right) \right]$ and $\operatorname{Im}\left[ \operatorname{Li}_3\left( e^{-2\pi i/3} \right) \right]$. Moreover, these values can be computed using the Fourier series of the Bernoulli polynomials. The upshot of this observation is that
$$ \operatorname{Re}\bigl[ \operatorname{Li}_2\bigl( e^{-2\pi i/3} \bigr) \bigr] = -\frac{\pi^2}{18}, \qquad
\operatorname{Im}\bigl[ \operatorname{Li}_3\bigl( e^{-2\pi i/3} \bigr) \bigr] = -\frac{2\pi^3}{81}. $$
Putting altogether, we end up with
$$ \lim_{\epsilon \to 0^+} \operatorname{Im}( B_{\epsilon} ) = -\frac{\pi^3}{2592}, $$
Conclusion. Combining all the efforts and using the relation
$$ I
= \lim_{\epsilon \to 0^+} \operatorname{Im}(J_{\epsilon})
= \lim_{\epsilon \to 0^+} \operatorname{Im}(A_{\epsilon} - B_{\epsilon}), $$
the desired equality is proved.

