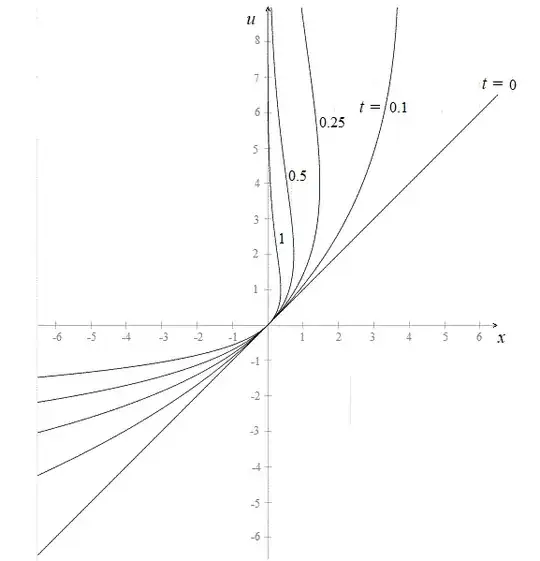
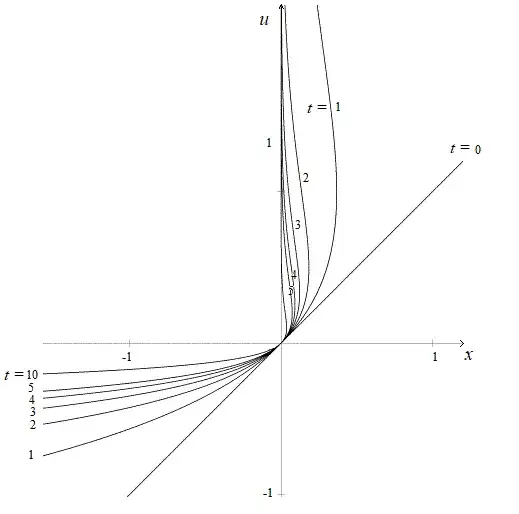
Consider the equation $u_t - x u u_x = 0$. with cauchy data $u(x,0) = x$. Solving this equation I see the characteristics are given by $x= r e^{-rt}$ for some $r$ and the solution is defined implicitly by
$$ x = u e^{-ut} $$
Using lambert function, one can solve for $u$. When plotting the characteristics, I see that after $t=4$ there are no characteristics. How do we find analytically the values of $t$ for which we have a smooth solution?
The characteristics are the curves $x = x_0 \exp (-x_0 t)$ for $x_0\in\Bbb R$, along which $u=x_0$ is constant (see e.g. this related post). Differentiating $x$ w.r.t. $x_0$, we find that $$ \frac{\text d x}{\text d x_0} = (1 -t x_0) \exp (-x_0 t) , $$ which vanishes at $t=1/x_0$. The smallest such positive value defines the breaking time $t_b = \inf 1/x_0 = 0$, which is only reached as $x_0 \to \pm\infty$. Hence, the solution keeps smooth. The solution can be expressed as $$x_0 = -W(-xt)/t = x\, e^{-W(-xt)} = u(x,t),$$ where $W$ is the Lambert W-function. This special function is real-valued if its argument $-xt$ is larger than $-1/e$. Hence, as represented in the $x$-$t$ plane below, the domain is bounded:
For positive abscissas $x>0$, we must have $t<1/(ex)$. Thus, if $t=4$, the solution is located at abscissas $x<1/(4e) \approx 0.092$, which may explain that you don't see any solution elsewhere. For negative abscissas $x<0$, there is no restriction at positive times $t>0>1/(ex)$.
I agree with your result : $$x=u\,e^{-u\,t}$$ This is the solution on the form of implicit equation.
Of course, if one want the explicit form the Lambert W function is required
$u(x,t)=-\frac{1}{t} W\left(-t\,x \right)\quad$ But we don't need it to plot $u(x,t)$.
Drawing the curves $u(x)$ for various $t$ is very easy, without special function. Plot the inverse function $x(u)$ , which is explicit. Then symmetry/rotation make the figure on the usual orientation.
The solutions remain smooth from $t=0$ up to large $t$.
Nothing special appears at $t=4$ and latter.
If you draw the curves with the Lambert W function instead of the above very simple method you avoid possible numerical artefact (Of course, with a sufficient accuracy of the numerical computation of the Lambert W function the results must be the same for the two methods).
