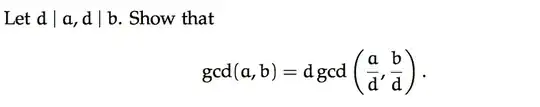0

enter image description here

I think the strategy for this problem would be i assume some arbitrary element is in gcd(a,b) and chase it into the rhs and then do it the other way around , but i am not sure how to even start this one.

H.B
  • 47
  • 7
  • Use the fact that $\gcd(u,v)$ is the smallest positive number in ${ux+vy:x,y\in\mathbb Z}$. – Dave Feb 18 '19 at 21:43
  • so would i have gcd(a,b)=ax+by=ax/d+by/d=dgcd(a/d,b/d)? how would the other direction go? – H.B Feb 21 '19 at 06:51

1 Answers1

0

We can rephrase the conditions as $a=p\cdot d$ and $b=q\cdot d$ with $p,q\in\mathbb{N}$.

Then $$\gcd(a,b)=\gcd(pd,qd)=d\cdot\gcd(p,q)=d\cdot\gcd(\frac{a}{d},\frac{b}{d})$$

Jonas De Schouwer
  • 535
  • 4
  • 11