How to find all the solutions for $\sum\limits_{i=1}^{n} \frac{1}{2^{k_i}}= 1$ for $k_i\in \Bbb{N}$ and $n$ a fixed positive integer?

Question

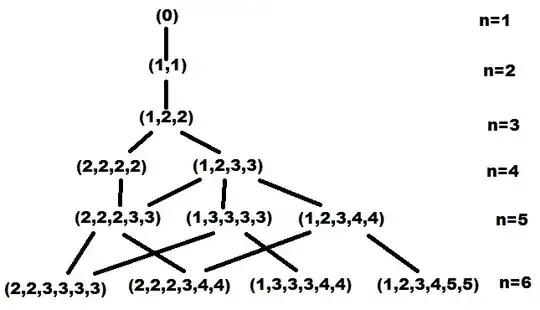
I got curious with the following: How can I find all the solutions for

$$\frac{1}{2^{k_1}} + \frac{1}{2^{k_2}} + \frac{1}{2^{k_3}} + \dots + \frac{1}{2^{k_n}}=1$$

for $k_i\in \Bbb{N}$ with $n$ a fixed positive integer? I thought about multiplying both sides by $2^{k_1} 2^{k_2}\dots 2^{k_n}$ but it looked useless at first sight. Is there some algorithm for that? Sorry if the question is too trivial, but I spent a while thinking and nothing came to my mind.

EDIT: I'm not sure this is actually number theory. Feel free to add or remove tags if it isn't.

One solution is $k_i=i$ for $1\le i\le (n-1)$ and $k_n=k_{n-1}$. — Keith Backman, Mar 05 '19 at 19:49
You can generate all the solutions (up to a rearrangement) by constructing the full binary trees with $n$ leaves. Then, assign values of $k_i$ to be the level of the $i$th leaf on the tree. — Theo Bendit, Mar 05 '19 at 20:06
An interesting extension of the question is the replace the sum with a limit to infinity, where the k series would have to go through all the natural numbers. — Mikael Jensen, Mar 06 '19 at 09:27
It would be nice also to just count the number of solutions: I posted a related question for that. — Fabius Wiesner, Mar 07 '19 at 08:50

score 3 · Answer 1 · answered Mar 05 '19 at 20:15

3

This image shows how to generate iteratively all solutions $(k_1, \dots, k_n)$ for all $n$, under the constraint $k_1 \le \dots \le k_n$.

The "sons" of every solution $(k_1, \dots , k_i, k_{i+1} \dots , k_n)$ are found by replacing $k_i$ with $(k_i+1, k_i+1)$ (under the constraint that $k_i < k_{i+1}$).

answered Mar 05 '19 at 20:15

Crostul

36,738
4
36
72

You missed $(1,2,4,4,4,4)$ for $n=6$ which is child of $(1,2,3,4,4)$. Also, $(1,3,3,3,4,4)$ is child of $(1,2,3,4,4)$ too. – Fabius Wiesner Mar 07 '19 at 14:33
@mbjoe You are right! Thanks for your comment. I'm sorry, but I will not modify the image... – Crostul Mar 07 '19 at 18:40

How to find all the solutions for $\sum\limits_{i=1}^{n} \frac{1}{2^{k_i}}= 1$ for $k_i\in \Bbb{N}$ and $n$ a fixed positive integer?

1 Answers1

Linked