Find value of $|z_2+z_3|$

Question

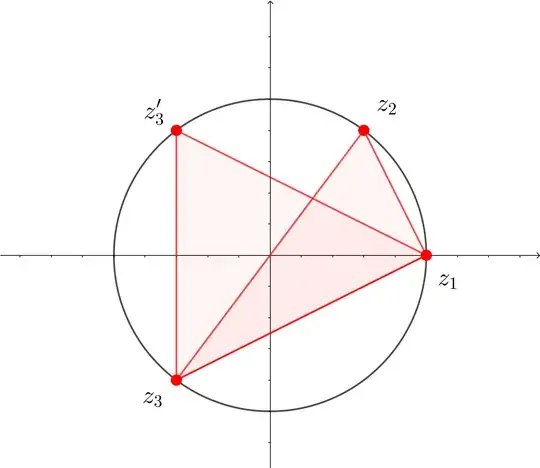
Given that complex numbers $z_1,z_2,z_3$ lie on unit circle and

$$|z_1-z_2|^2+|z_1-z_3|^2=4$$ Then find value of $|z_2+z_3|$

My try:

We can take $z_1=e^{i\alpha}$, $z_2=e^{i\beta}$ and $z_3=e^{i\gamma}$

So we have

$$|z_1-z_2|=2\sin\left(\frac{\alpha-\beta}{2}\right)$$

$$|z_1-z_3|=2\sin\left(\frac{\alpha-\gamma}{2}\right)$$

So we get:

$$\sin^2\left(\frac{\alpha-\beta}{2}\right)+\sin^2\left(\frac{\alpha-\gamma}{2}\right)=1$$

Now we have:

$$|z_2+z_3|=2\cos\left(\frac{\beta-\gamma}{2}\right)$$

Any help here?

Answer 1

As pointed out in comment by Stancek, whom I thank, my previous answer was not correct since it only reported one solution, that was indenpendent on the choice of $z_1$, $z_2$ and $z_3$, i.e $$|z_2+z_3|=0,$$ easily found by Pythagorean Theorem.

The general solution can be determined as follows. Use the fact that $|z|^2 = zz^*$, to re-write the equation in the form $$|z_1|^2 - 2\Re\{z_1z_2^*\} + |z_2|^2 + |z_1|^2 - 2\Re\{z_1z_3^*\} + |z_3|^2=4.$$ Since the points lie on the unit circle, the equation then simplifies to $$ \Re\{z_1z_2^*\} = -\Re\{z_1z_3^*\}.$$ If you set $z_1 = 1$ you get $$\Re\{z_2\} = -\Re\{z_3\}.$$ Which yields the two solutions $$z_3 = -z_2$$ and $$z_3 = -z_2^*.$$ The first solution leads to $$\boxed{|z_2+z_3|=0},$$ that is to $z_1$, $z_2$, and $z_3$ being vertices of a right-angled triangle. The second one, in the case $z_1=1$ can be expressed as $$|z_2+z_3|= 2\left|\Im\{z_2\}\right|.$$ Taking into account the arbitray phase of $z_1$ yields $$\boxed{|z_2+z_3|= 2\left|\Im \left\{z_1z_2^*\right\}\right|}.$$

Answer 2

Note that if $|z|=1$, then $\overline{z}=1/z$. Thus for $z_1$, $z_2$, and $z_3$ on the unit circle, we have

$$\begin{align} |z_1-z_2|^2+|z_1-z_3|^2 &=\left(z_1-z_2\right)\left({1\over z_1}-{1\over z_2}\right)+\left(z_1-z_3\right)\left({1\over z_1}-{1\over z_3}\right)\\ &=4-\left({z_1\over z_2}+{z_2\over z_1}+{z_1\over z_3}+{z_3\over z_1} \right)\\ &=4-\left((z_1^2+z_2z_3)(z_2+z_3)\over z_1z_2z_3 \right) \end{align}$$

It follows that $|z_1-z_2|^2+|z_1-z_3|^2=4$ if and only if $(z_1^2+z_2z_3)(z_2+z_3)=0$. Since we can always arrange for $z_1^2=-z_2z_3$ on the unit circle, $|z_2+z_3|$ can take any value between $0$ and $2$.

Answer 3

Hint: Writing $$\frac{\beta-\gamma}{2}=\frac{\beta-\alpha}{2}+\frac{\alpha-\gamma}{2}$$ and combing this with trigonometric identity for the sum of cosine $$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$$ we get \begin{align}\cos\left(\frac{\beta-\gamma}{2}\right)&=\cos\left(\frac{\beta-\alpha}{2}+\frac{\alpha-\gamma}{2}\right)\\ &=\cos\left(\frac{\beta-\alpha}{2}\right)\cdot\cos\left(\frac{\alpha-\gamma}{2}\right)-\sin\left(\frac{\beta-\alpha}{2}\right)\cdot\sin\left(\frac{\alpha-\gamma}{2}\right).\end{align} Now rewrite the identity $$\sin^2\left(\frac{\alpha-\beta}{2}\right)+\sin^2\left(\frac{\alpha-\gamma}{2}\right)=1$$ as $$\sin^2\left(\frac{\alpha-\beta}{2}\right)=1-\sin^2\left(\frac{\alpha-\gamma}{2}\right)=\cos^2\left(\frac{\alpha-\gamma}{2}\right),$$ and plug this into the previous to conclude.