1

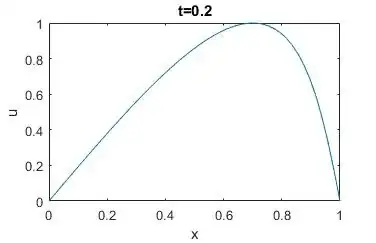
Using the equation $u \equiv u ( x , t ) = u _ { 0 } ( x - t u ( x , t ) )$ to compute $u \left( T , x _ { j } \right)$ for the Burgers equation, where the Burgers equation is $u _ { t } + \left( \frac { 1 } { 2 } u ^ { 2 } \right) _ { x } = 0$ with $u ( 0 , x ) = u _ { 0 } ( x )$ and initial conditions $u _ { 0 } ( x ) = \sin ( \pi x )$

I think we have to use the fixed point equation $y = y + c \left( y - u _ { 0 } \left( x _ { j } - T y \right) \right)$ for a suitable $c$.

I don't know how to go about this and I have to implement this in Matlab as well. How to proceed? Thanks.

EditPiAf
  • 20,898
Junia Shelomi
  • 23

1 Answers1

3

Indeed, the solution deduced from the method of characteristics satisfies $u = u_0(x - ut)$, to be solved for each point $(x,t)$ of interests. One approach is fixed-point iterations:

x = linspace(0,1,50);
u = x;
t = 0.2;
for i=1:length(x)
    fun = @(u) sin(pi*(x(i)-u*t));
    u0 = 0;
    err = abs(fun(u0)-u0);
    n = 0;
    while (err>1e-10)&&(n<100)
        u0 = fun(u0);
        err = abs(fun(u0)-u0);
        n = n+1;
    end
    u(i) = u0;
end
plot(x,u);
xlabel('x');
ylabel('u');
title(strcat('t=',num2str(t)));

with the following output:

output

A native Matlab method based on a root-finding algorithm is provided here.

EditPiAf
  • 20,898