Conservation law $A_t + (A^{3/2})_x = 0$ for flood water wave

Question

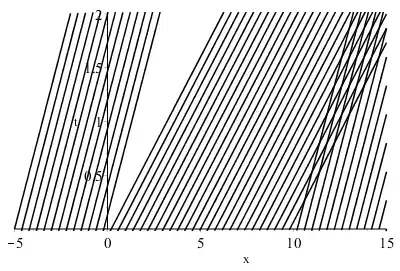
The flood wave in a river follows the conservation law $$ A_t + (A^{3/2})_x = 0 $$ where $A(x,t)$ is the cross sectional area of the water at the location $x$ and time $t$. A sudden heavy rain creates a flood with river cross sectional area along its path as follows (set it as $t=0$) $$ A(x,0) = \left\lbrace\begin{aligned} &1 && x\leq 0 \\ &4 && 0 < x \leq 10\\ &1 && x> 10 \end{aligned}\right. . $$

(a) Find and draw the characteristics of the equation.

(b) Find the solution of cross sectional area along the river at $t=1$.

(c) Assume a town is located at $x=31$, when will the flood crest reach it?

TRY:

First, we write the PDE as $A_t + \frac{3}{2} A^{1/2} A_x = 0 $

Now, solving this equation using method of characteristiscs, we obtain

$$ x = \frac{3}{2} \sqrt{ A(r,0) } t + r $$

for characteristics equation and solution is implicity given by

$$ A(x,t) = \phi ( x - 3/2 \sqrt{ A } s ) $$

where $\phi(x) = A(x,0) $. So, we have characteristic are described by

$$ x = \begin{cases} 3/2 t + r,& r \leq 0 \\ 3t + r,& 0 < r \leq 10 \\ 3/2t+r,& r > 10 \end{cases} $$

am I correct so far?

Answer 1

Here is a plot of the characteristic curves in the $x$-$t$ plane as deduced from the initial data:

The flux $A \mapsto A^{3/2}$ is convex for positive cross sectional area $A$. Hence, the classical theory for weak entropy solutions of conservation laws applies. One can observe that

• At $x=0$, characteristics separate. A rarefaction wave is created, which waveform $v(x/t)$ is given by the reciprocal of the function $A \mapsto \frac{3}{2}\sqrt{A}$, i.e., $v(x/t) = \frac{4}{9}(x/t)^2$.

• At $x=10$, characteristics intersect. According to the Lax entropy condition, a shock wave is created, which speed $s$ satisfies the Rankine-Hugoniot condition $s = {(4^{3/2}-1^{3/2})}/{(4-1)}= \frac{7}{3}$.

Therefore, the entropy solution for small positive times reads $$ A(x,t) = \left\lbrace \begin{aligned} & 1 && x \leq \tfrac{3}{2} t \\ & \left(\tfrac{2x}{3t}\right)^2 && \tfrac{3}{2} t \leq x \leq 3 t\\ & 4 && 3 t \leq x \leq 10 + \tfrac{7}{3} t \\ & 1 && x \geq 10 + \tfrac{7}{3} t \end{aligned} \right. $$ which is valid at $t=1$. Indeed, the rarefaction wave does not catch the shock before the time $t^*$ such that $3 t^* = 10 + \tfrac{7}{3} t^*$, i.e., $t^* = 15$. The shock wave will reach $x=31$ at the time $21/\frac{7}{3} = 9$ at which the previous solution is still valid ($t < t^*$).