While reading the book on Forms and connection ,I am stuck with following defination of manifold.I am stuck at the part after defining function $f$ for submersion. Can anyone explain me this defination using example?
- 129
-
See chapter 5 from the book Jhon M.Lee introduction to smooth manifold. – Bey Alexander Mar 23 '19 at 19:09
1 Answers
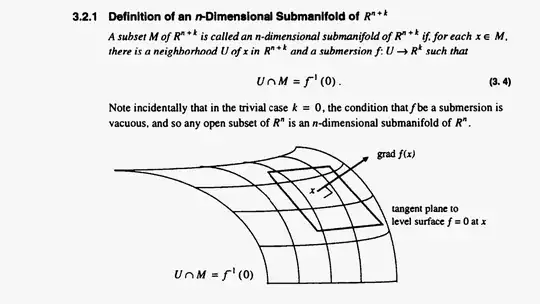
The idea is to see the submanifold as the solution to a system of $k$ equations with $n+k$ unknowns, at least locally. Requiring that $f$ be a submersion is asking that the equations not be redundant.
Consider the example of a circle in $\mathbb{R}^2$: you can think of it as the solutions to the equation $$ x^2 + y^2 = 1. $$ In this example you can take $U$ to be $\mathbb{R}^2 \setminus \{ 0 \}$ and your submersion to be $f \colon U \to \mathbb{R}$ by $f(x,y) = x^2+y^2-1$.
Notice that the differential of $f$ is $2x dx + 2y dy$, which vanishes only at the origin, so this is a submersion.
We can consider a circle inside of $\mathbb{R}^3$ also, for instance, by taking a single set $U = \mathbb{R}^3 \setminus ( \{ (0,0) \} \times \mathbb{R} )$ and taking $ f \colon U \to \mathbb{R}^2$ by $f(x,y,z) = (x^2+y^2-1, z)$. The circle is then the set of points with $z=0$ and $x^2+y^2 = 1$.
Now, the idea of allowing yourself several open sets and several different submersions is that your submanifold might only look like this locally. (If it is globally obtainable by a submersion, it has what is called a trivial normal bundle. If the submanifold is something non-orientable, like a Klein bottle or real projective space sitting inside $\mathbb{R}^4$, you will need multiple open sets and multiple functions. There are other examples, as discussed in this related question: Manifold embedded in euclidean space with nontrivial normal bundle)
- 3,243
-
Great answer!! One question. What does the statement $$""U \cap M=f^(-1)(0)$$? – Abhi7731756 Mar 24 '19 at 01:55
-
1@Abhi7731756 it's mean you can see your submanifold locally as level sets for some submersion (it's a one criteria of proving a set is submanifold). – Bey Alexander Mar 24 '19 at 02:57
-
@Abhi7731756, are you asking what the notation $f^{-1}(0)$ means? It means the set of points ${ (x_1, \dots, x_n) \in U \subset \mathbb{R}^n , | , f(x_1, \dots, x_n) = 0 }$. I'm thinking of this as the set of solutions to the equation $f(x_1, \dots, x_n) = 0$.
The statement $U \cap M = f^{-1}(0)$ then means that the part of $M$ that is in the open set $U$ is given by set of points that have $f(x_1, \dots, x_n) = 0$.
– Sam Lisi Mar 24 '19 at 17:19