Volume of a 3D simplex

Question

I want to find the volume of the following simplex

$$B := \{ (x,y,z) \in \mathbb{R^3} \mid x \geq 0, y \geq 0, z \geq 0, x+y+z \leq 2 \}$$

I tried to do it by evaluating a double integral but I'm stuck with finding the right bound of integration. I tried the following:

$$\int_{0}^{2} \int_{0}^{2-z-x} (2-z-y) \, \mathrm d y \mathrm d x \mathrm d z$$

But I'm really unsure if this is the right approach. Can anyone point me in the right direction? Or give me a link to some resources where I can learn more about this topic?

Answer 1

One way is using a change of variables.

You can transform $(x,y,z)\to(u,v,w)$ such that $$u=x+y+z\,,\,uv=x+y\,,\,uvw=x$$

So that, $$x,y,z>0\,,\,x+y+z<2\implies 0<u<2\,,\,0<v,w<1$$

Absolute value of jacobian of transformation is $$|J|=u^2v$$

Hence the volume is

\begin{align} \iiint_B\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z =\int_0^1\int_0^1\int_0^2 u^2v\,\mathrm{d}u\,\mathrm{d}v\,\mathrm{d}w \end{align}

Answer 2

Two different methods of solution :

First (analytical) method :

First of all, in this kind of volume calculation,

• a) either you work with a triple integral as @StubbornAtom as done in his answer

• b) or (often preferable if it is possible) express your volume as the volume over a certain domain $D$ under a certain surface with equation $z=f(x,y)$, as a double integral :

$$\int\int_D f(x,y)dxdy$$

This is what we are going to do here with $f(x,y)=z=2-x-y$:

$$\int_{y=0}^{y=2}\left(\int_{x=0}^{x=2-y}(2-x-y)dx\right)dy$$

(please note the parentheses ; bounds of integration can be understood when looking at Fig. 1).

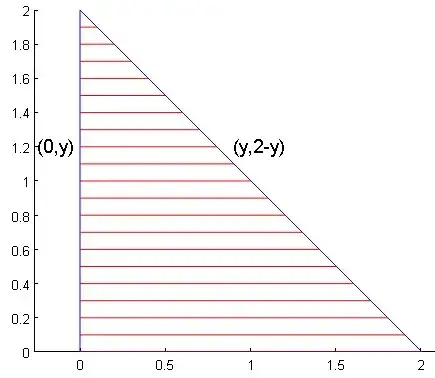
Fig. 1 : The way the domain of integration $D$ (in plane $xOy$) is swept, for a given $y$, from $x=0$ to $x=2-y$.

The integrand $(2-y)-x$ of the internal integral has an antiderivative (with respect to variable $x$) : $$(2-y)x-\frac{x^2}{2} \ \text{to be taken between} \ x=0 \ \text{and} \ x=2-y$$

giving for the final value of the internal integral

$$\frac{(2-y)^2}{2}$$

It now remains to compute : $\int_{y=0}^2 \frac{(2-y)^2}{2}dy$ ; its value is

$$\frac{-(2-y)^3}{6} \ \text{to be taken between} \ y=0 \ \text{and} \ y=2$$

which finally gives the result $\frac43$

---

Second (geometrical) method :

This volume is a tetrahedron $OABC$ that can be considered as well as a three-sided pyramid (lying on one of its sides), with equilateral triangle $ABC$ (with sidelength $2\sqrt{2}$) as its base. The centroid of this base equilateral base has coordinates the mean of coordinates of $A,B,C$:

$$I=\tfrac13((2,0,0)+(0,2,0)+(0,0,2))=(\tfrac23,\tfrac23,\tfrac23).$$

The height of this pyramid is distance $h=OI=2/\sqrt{3}$.

It remains to apply the formula giving the volume of a pyramid knowing the area $S$ of its base and its height $h$ :

$$V=\tfrac13 \times S \times h = \tfrac13 \times 2 \sqrt{3} \times \tfrac{2}{\sqrt{3}}=\tfrac43.$$

as in the first solution.

Answer 3

Regarding the geometric approach to finding the volume, an easier way is to visualise the pyramid whose height vector is along the $z$-axis from 0 to 2. Then the base is just a triangle with width 2 and length 2, so the volume is $$V = \frac{1}{3}Ah = \frac{1}{3} \times (\frac{1}{2} \times 2 \times 2) \times 2 = \frac{4}{3} $$

Answer 4

We start from $$x\geq 0, y\ge 0, z\ge 0, x + y + z\le 2\implies 0\le z\le 2.$$ Now, fixing $z$: $$x\geq 0, y\ge 0,x + y\le 2 - z\implies 0\le y\le 2 - z.$$ Finally, fixing $y$: $$x\geq 0, x\le 2 - y - z\implies 0\le x\le 2 - y - z.$$