Doubts about supremum.

Question

Need help in vetting my answers for Q. 1 in chap. 2 in CRM series book by MAA: Exploratory Examples for Real Analysis, By Joanne E. Snow, Kirk E. Weller. .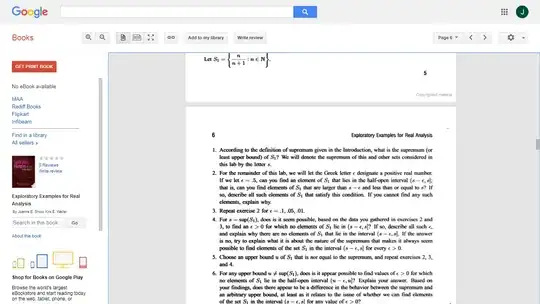

Let $S_1 = \frac n{n+1} : n \in \mathbb{N}$

1. What is the supremum of $S_1$. Denote it by $s$.

As denominator is larger than numerator, so consider the first few values:

$$\begin{array}{c|c|} & \text{$n\in \mathbb{N}$}& \text{$\frac n{n+1}$}\\ \hline a & 1& \frac12\\ \hline b & 2& \frac23\\ \hline c & 3& \frac34\\ \hline d & 4& \frac45\\ \hline \end{array}$$ The function is monotonic under reals, except at $n=-1$. So, monotonic under smaller class of naturals too.
Taking derivative helps by stating maxima at $s=1$.
The upper bound will be all naturals in $[1,\infty)$

2. Let $\epsilon$ be a positive real number. Let $\epsilon=0.5$, can you find an element of $S_1$ that lies in the half open interval $(s - \epsilon, s]$; i.e. can you find an element of $S_1$ that are larger than $s - \epsilon$ & less than or equal to $s$? If so, describe all such elements of $S_1$ that satisfy this condition. If you cannot find any such elements, explain why?

Given $s=1, \epsilon=0.5$, it translates to :
can you find an element of $S_1$ in $0.5 \lt S_1 \le 1$?
Edit :
Given $s=1, \epsilon=0.5$, it translates to :
can you find an element of $S_1 \cap (0.5,1]$, where $S_1=\{\frac{n}{n+1}: n \in \mathbb{N} \}$?

Yes, all except the first element of the series, i.e. $S_1 \cap (0.5,1]=\{\frac{n}{n+1}: n \in \mathbb{N}, n\gt 1 \}$.

Extra :
Want to solve for $0.5 \lt \frac{n}{1+n} \le 1 $.
Taking the $l.h.s.$, get $\frac{n}{1+n}\gt \frac 12 \implies n \gt 1$.
Taking the $r.h.s.$, get $\frac{n}{1+n}\le 1 \implies n \le 1+n \implies 0 \le 1$.
The $l.h.s.$ yields correct result, i.e. for all except the first term; while the $r.h.s.$ yields a vacuously true stmt. only.

3. Repeat exercise $2$ for $\epsilon=0.1, 0.05, 0.01$.

1. $\epsilon=0.1$:
   Given $s=1, \epsilon=0.1$, it translates to :
   can you find an element of $S_1$ in $0.9 \lt S_1 \le 1$?

Edit :
Given $s=1, \epsilon=0.1$, it translates to :
can you find an element of $S_1 \cap (0.9,1]$, where $S_1=\{\frac{n}{n+1}: n \in \mathbb{N} \}$?

Yes, $\frac {10}{11} = 1-\frac {1}{11} =1-0.0\overline{90} =0.\overline{90}$, is the first such element for $n=10$.
In other words, $S_1 \cap (0.9,1]=\{\frac{n}{n+1}: n \in \mathbb{N}, n\ge 10\}$.

Extra :
Want to solve for $0.9 \lt \frac{n}{1+n} \le 1 $.
Taking the $l.h.s.$, get $\frac{n}{1+n}\gt \frac 9{10} \implies n \gt 9$.
Taking the $r.h.s.$, get $\frac{n}{1+n}\le 1 \implies n \le 1+n \implies 0 \le 1$.
The $l.h.s.$ yields correct result, i.e. for all $n\gt 9$.

2. $\epsilon=0.05$:
   Given $s=1, \epsilon=0.05$, it translates to :
   can you find an element of $S_1$ in $0.95 \lt S_1 \le 1$?

Edit :
Given $s=1, \epsilon=0.05$, it translates to :
can you find an element in the set $S_1 \cap (0.95,1]$, where $S_1=\{\frac{n}{n+1}: n \in \mathbb{N}\}$?

Yes, $\frac {20}{21} = 1-\frac {1}{21} =1-0.\overline{047619}= 0.95\overline{238095}$, is the first such element for $n=10$.
In other words, $S_1 \cap (0.95,1]=\{\frac{n}{n+1}: n \in \mathbb{N}, n\gt 19 \}$.

Extra :
Want to solve for $0.05 \lt \frac{n}{1+n} \le 1 $.
Taking the $l.h.s.$, get $\frac{n}{1+n}\gt \frac 1{20} \implies n \gt 19$.
Taking the $r.h.s.$, get $\frac{n}{1+n}\le 1 \implies n \le 1+n \implies 0 \le 1$.
The $l.h.s.$ yields correct result, i.e. for all $n\gt 19$.

3. $\epsilon=0.01$:
   Given $s=1, \epsilon=0.01$, it translates to :
   can you find an element of $S_1$ in $0.99 \lt S_1 \le 1$?

Edit :
Given $s=1, \epsilon=0.01$, it translates to :
can you find an element in the set $S_1 \cap (0.99,1]$, where $S_1==\{\frac{n}{n+1}: n \in \mathbb{N} \}$?

Yes, $\frac {100}{101} = = 1-\frac {1}{101} =1-0.\overline{0099}=0.99\overline{0099}$, is the first such element for $n=100$. In other words, $S_1 \cap (0.95,1]=\{\frac{n}{n+1}: n \in \mathbb{N}, n\ge 100 \}$.

Extra :
Want to solve for $0.01 \lt \frac{n}{1+n} \le 1 $.
Taking the $l.h.s.$, get $\frac{n}{1+n}\gt \frac 1{100} \implies n \gt 99$.
Taking the $r.h.s.$, get $\frac{n}{1+n}\le 1 \implies n \le 1+n \implies 0 \le 1$.
The $l.h.s.$ yields correct result, i.e. for all $n\gt 99$.

4. For $s = \sup(S_1)$, does it seem possible, based on the data you have gathered in exercise $2$ and $3$, to find an $\epsilon\gt 0$ for which no elements of $S_1$ that lie in $(s - \epsilon, s]$? If so, describe all such $\epsilon$, and explain why there are no elements of $S_1$ that lie in the interval $(s - \epsilon, s]$? If the answer is no, try to explain what it is about the nature of the supremum that makes it always seem possible to find elements of the set $S_1$ in the interval $(s- \epsilon, s]$ for every $\epsilon\gt 0$.

Not clear, as for very small $\epsilon$, there should be $n\rightarrow \infty$. But, if consider supremum for such non-attainable values (of $n$ in domain) only then get its value of $s=1$.

So, the exercise must be referring to the ability of supremum as a limiting value, for $n\rightarrow \infty$.

5. Choose an upper bound $u$ of $S_1$ that is not equal to the supremum, & repeat exercises $2,3$, and $4$.

Have doubt that given the domain ($n$) under naturals, can the set $u$ have reals also.

Am taking $u$ using both approaches :
1. to consist of naturals only,
2. to consist of reals only.

Am showing using both approaches:

1. Let us take $u = 2$ as the next value in $u$ after $s$.
   

I am unable to attempt even.

2. Do not know what to take as actual next value to $s=1$, so take $u = 1.0001$

I am unable to attempt even.

Edit :
$u$ is concerned with range, & hence can be in reals, or whatever the function maps to.

$u,s$ are related s.t. $u\gt s$. Need find $S_1 \cap (u-\epsilon, u]$. The lower bound of the interval $(u-\epsilon, u]$ is open, so only way for $S_1 \cap (u-\epsilon,u]\ne \emptyset$ is to have $(u-\epsilon) \lt s$.

6. For any upper bound $u\ne \sup(S_1)$, does it appear possible to find the values of $\epsilon\gt 0$ for which no elements of $S_1$ lie in the half-open interval $(u-\epsilon, u]$? Explain your answer. Based on your findings, does there appear to be a difference in the behavior between the supremum and an arbitrary upper bound, at least as it relates to the issue of whether we can find relates to the issue of whether we can find elements of the set $S_1$ in the interval $(s-\epsilon, s]$ for any value of $\epsilon\gt 0$.

I am unable to attempt even, as unable to answer for Q. 5.

Edit :
The first part concerns with showing possibility of values of $\epsilon\gt 0$ s.t. $S_1,\cap (u-\epsilon, u]=\emptyset$.

This is true if $u-\epsilon \ge s(=1)\implies \epsilon\le u-1$, & the selected answer has taken value of $\epsilon$ accordingly as $\frac{u-1}2$.
A general approach is to either take :
(i) $\epsilon = \frac{u-1}k, k \gt 0, k \in \mathbb{R}{+}$,
(ii) $\epsilon = u-1-k, k \gt 0, k \in \mathbb{R}{+}$

The hypothesis is: There exists an element of $x_i\in S_1$ such that $x_i\in (u-\varepsilon_i, u], \forall \varepsilon_i\in [0,u]$?

Will prove (in both cases) by contradiction, the hypothesis false.

But to simplify, will remove $i$ subscript; else need $n_i$. This unnecessarily complicates proof. Removing the subscript still conveys the same meaning.

(i) $\exists n \in \mathbb{N}, x = \frac{n}{n+1}$ (using $\exists n \in \mathbb{N}$, as depending on constraints on $\epsilon$, some values of $n$ might be invalid), we have $x\leq 1$. The limit of the interval $(u-\epsilon, u]$, of interest is lower one, i.e.: $u-\epsilon = u-\frac{u-1}k = \frac{1+(k-1)u}k \gt \frac{1+s}{k}(=\frac 2k)$.
The least value of lower limit of the interval is $\frac 2k$.

So, for given $k$, hypothesis is true iff $\frac 2k \lt x \implies k \gt \frac 2x\implies k \gt \frac{2(n+1)}n\implies k \gt 2 (1+\frac 1n)$.
This condition on $k$ should be achievable for a given $n$, e.g. for $n=5, k \gt 2(1+\frac 15) \implies k \gt \frac{12}5$.
This condition unless specified, the hypothesis is invalid/false $\forall x \in S_1$.
Hence, $x \notin (u-\varepsilon, u]$, for all $x\in S_1$.

(ii) similar to above

Answer 1

Let $u$ be a number greater than $1$, $1<u$. Is there an $\varepsilon >0$ such that $S_1 \cap (u-\varepsilon, u] = \varnothing$?

Sure there is, take $u-1>0$ and set $\varepsilon = \frac{u-1}{2}$.

Is there an element of $x\in S_1$ such that $x\in(u-\varepsilon, u]$?

Since $x = \frac{n}{n+1}$ for some $n \in \mathbb{N}$ we have $x\leq 1 < u-\varepsilon = u-\frac{u-1}2 = \frac{1+u}2$.

Hence, $x \notin (u-\varepsilon, u]$, for all $x\in S_1$.

Basically, if $s = Sup(S_1),\quad \forall \varepsilon >0, S_1 \cap (s-\varepsilon,s] \neq \varnothing$.

On the other hand, if $u$ is an upper bound which is not the supremum, then there exists a certain $\varepsilon_0>0$ such that $S_1 \cap (u-\varepsilon_0,u] =\varnothing$.

Answer 2

1. Testing a few data point doesn't tell us about the monotonicity. Also, we do not need differentiation actually.

$$\frac{n}{n+1}=\frac1{1+\frac1n}$$

Hence as $n$ increases, $\frac1n$ decreases, hence $\frac1{1+\frac1n}$ increases.

Also, $\lim_{n \to \infty} \frac1{1+\frac1n}=1$. Hence the supremum is $1$.

2. I don't think you want to write $0.5< S_1< 1$, comparing sets with number directly might need more clarification. You could have write it as $S_1 \cap (0.5,1]=\{\frac{n}{n+1}: n \in \mathbb{N}, n> 1 \}$.

To see it quickly, $$\frac{n}{n+1}>1-\frac12=\frac12$$

$$2n>n+1$$

$$n>1$$

3. Similar comments for question $3$. In fact, given $\epsilon \in (0,1)$, you might want to solve for $\frac{n}{1+n}>1-\epsilon$.

4. You can't find $\epsilon$ in general. Clearly, we have $s \notin S_1$. Suppose such $\epsilon$ exists, then $s-\epsilon$ would be an upperbound to $S_1$ which contradicts $s$ being the smallest upperbound.

5. $S_1$ is a subset of the set of real number. Whether $(u-\epsilon, u)\cap S_1 $ is non-empty would depends on how small $\epsilon$ is. If $u-\epsilon >1$, then the intersection will be empty.

Some comments for your edit:

Notice that you are repeating working multiple times. Try to do it just once generally.

$$\frac{n}{n+1}>1-\epsilon$$

$$n> n+1-\epsilon n -\epsilon$$

$$n>\frac{1-\epsilon}{\epsilon}=\frac1{\epsilon}-1$$

For part $5$, you are told to choose an upper bound $u$. You did not follow the instruction. Learn to only give the main points as concise as possible, avoid irrelevant stuff.

For part $6$. Again, learn to focus on answering the question. The question is for every $u$, can you find an $\epsilon$ that satisfy certain condition. The answer is positive as illustrated from the accepted answer. I would stop reading after the line that begins with $(i)$. The attempt to generalize it unfortunately didn't work out as you did not consider what happens as $k \in (0,1)$ carefully for the first case. You might have justified it later on how to pick $k$ but I would have stopped reading from the first line thinking that you claim any positive $k$ works. Also, your attempt for case $2$, what if $k$ is very large?

Edit:

Let $u=2$, $s=1$, $k=0.1$, $\frac{u-s}{k}=10$. $(u-\epsilon, u)$ would intersect with $S_1$. You might want to pick $k \ge 1$.