Here is a geometric construction of the foci and latus rectum of an ellipse based on the Dandelin spheres:
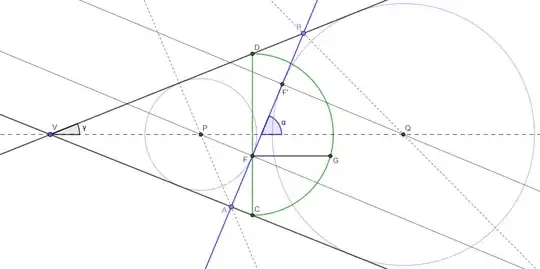
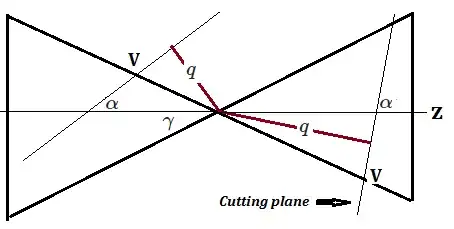
Given a cone with vertex at $V$ and semi-vertex angle $\gamma$ cut by a plane at angle $\alpha$ to the axis of symmetry,
in a plane through the axis of symmetry perpendicular to the cutting plane
the cutting plane intersects the cone at points $A$ and $B$
so that $AB$ is the major axis of the ellipse.
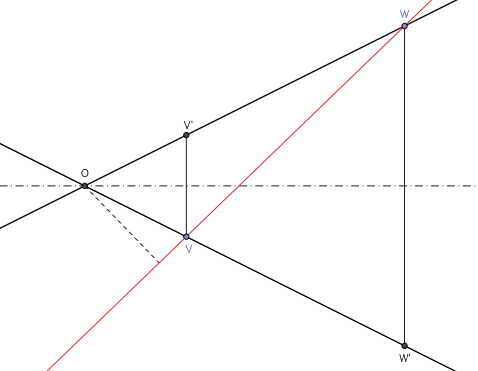
Bisect angle $\angle VAB$ and let $P$ be the intersection of the angle bisector with the axis of symmetry. Drop a perpendicular from $P$ to $AB$ intersecting $AB$ at $F.$
Then $F$ is a focus of the ellipse and $PF$ is a radius of the corresponding Dandelin sphere.
The other focus is similarly constructed by bisecting the angle $\angle B$ as shown in the figure (the other bisector would give us $P$ again),
finding the intersection $Q$ of the bisector and the axis of symmetry,
and dropping a perpendicular from $Q$ to $F'$ on $AB$; then $F'$ is the other focus
and $QF'$ is a radius of its Dandelin sphere.
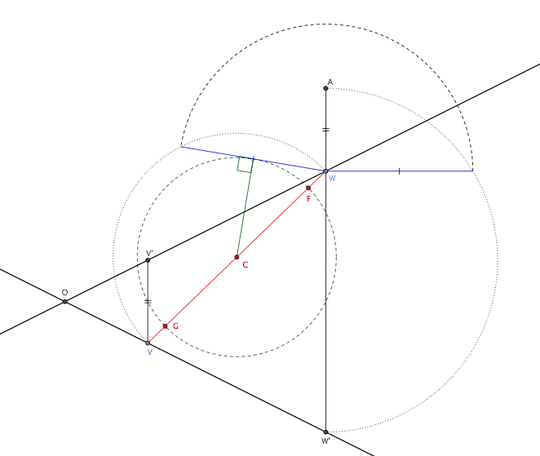
A plane through $F$ perpendicular to the axis of symmetry intersects the cone in a circle perpendicular to the plane of the figure,
with diameter $CD$ in the plane of the figure.
The semicircle $CD$ in the plane of the figure is congruent to one half of that circle.
Construct a line through $F$ perpendicular to the diameter $CD$ intersecting the semicircle at $G.$ Then $FG$ is the semi-latus rectum.
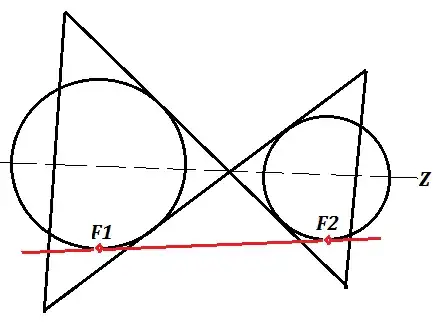
There is a corresponding construction for the foci and semi-latus rectum of a hyperbola.
The construction for the parabola has only one sphere and one focus.