1

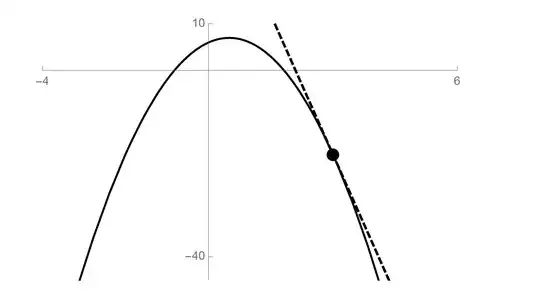
enter image description here

The figure shows the graph $f(x)=-2x^2+4x+6$ along with the tangent line at the point $(x,y)$

The given point has a nice property: the slope fo the tangent line is equal to the y-value at that point. Find the x-coordinate.

So the slope of the tangent line is the derivative which in this case would be $-4x+4$

This derivative is equal to the y-value at that point. So i will set the two equations equal to each other. .

$-2x^2+4x+6=-4x+4$

$-2x^2+8x+2=0$

$-2(x^2-4x-1)=0$

$x=2\pm\sqrt{5}$ Reject the negative so it is $2+\sqrt{5}$

Is this correct?

user477465
  • 720
  • 3
    It looks good to me. – José Carlos Santos Jun 01 '19 at 11:13
  • Note that the negative value of $x$ is the $x$ coordinate of a point where the $y$ coordinate of the graph and the slope of the graph are equal and positive, unlike the point shown in the figure where the $y$ coordinate is negative. In other words, there are two solutions to the words describing the problem, and you found both of them, but only one matches the picture. – David K Jun 01 '19 at 11:37

0 Answers0