Compare graphs of the two functions - the $\color{green} {green}$ one is for $\,\color{green}{y=\sin(x)}\ $ for $\color{green}x$ in radians, the $\color{red} {red}$ one is for $\color{red}{y=\sin(x)}\ $ for $\color{red}x$ in degrees:
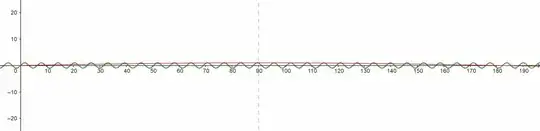
Here are the same graphs, but separated one from the other to better differentiate one from the other:
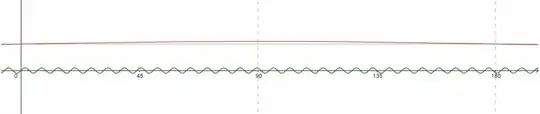
You may see, that the appearance of the $\color{red}{red}$ graph is almost horizontal line, with the maximum $\color{red}1$ at $\color{red}{x=90^o}$, because $\, \color{red}{\sin(90^o)= 1}$.
Now, the derivative in the arbitrary point $x$ is the slope of the tangent to the graph at the point $[x, \sin x]$.
You may see, that the slopes are not the same for the most $x$. It is even impossible, because the slope of the red $\,\color{red}{\sin(x)}$ is always damn near $\color{red}0$ (more precisely, it varies from cca $\color{red}{-0.017}$ to cca $\color{red}{+0.017}$), whereas the slope of green $\color{green}{\sin(x)}$ varies from $\color{green}{-1}$ to $\color{green}{+1}$.

