3

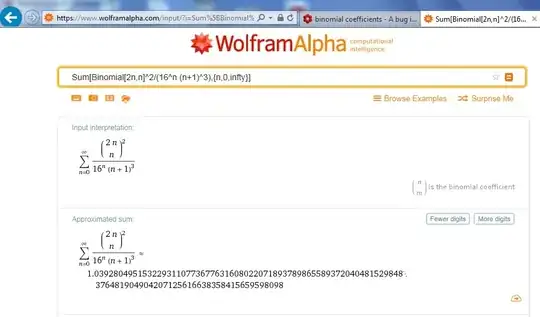
While verifying this MSE answer, I may have come across a bug in Wolfram Alpha. It evaluates the sum below as,

$$\qquad A=\sum_{n=0}^\infty\frac{\binom{2n}{n}^2}{16^n(n+1)^3}=1.03928049\color{red}{51}\dots$$

(press the "More digits" button) while it evaluates this generalized hypergeometric as,

$$B = \,_4F_3\big(\tfrac12,\tfrac12,1,1;\,2,2,2;\,1\big) = 1.03928049\color{red}{67}\dots\quad$$

The problem is it is supposed to be the case that

$$A=B=C$$

In fact, as the MSE answer points out, the closed-form is,

$$C=\frac{48}{\pi}+16\ln(2)-\frac{32G}{\pi}-16= 1.03928049\color{red}{67}\dots\quad$$

so that is the correct numerical value.

Q. Why does WolframAlpha give a wrong numerical evaluation for $A$?

Context of problem: I need 20, 30, or more correct digits for an integer relations algorithm to work and find a closed-form.

Screenshot below. This is about 100 digits, everything after the $8$th decimal place is wrong.

enter image description here

Tito Piezas III
  • 54,565
  • 6
    First of all, I wouldn't call that "a bug". It is just a matter of how good an approximation is. Second, WA has quite a few mistakes in several things...but this doesn't seem to be one of them, according to what you write. Approximating up to eight digits after the decimal point seems to me pretty good. – DonAntonio Jun 07 '19 at 17:00
  • 1
    I would guess WolframAlpha is using NSum[...] to get 'approximated sums', but when you do More Digits it might switch to using N[Sum[...]] to get an approximation of the exact sum (a hypergeometric function). If you use NSum in Mathematica itself, it warns about failure to converge. – Kyle Miller Jun 07 '19 at 17:28
  • @DonAntonio: It is just a disappointment. Sometimes WA just yields a few digits, and you know that is all the accuracy it can muster. But for this sum, it gave almost 100 digits, but I knew the numerical evaluation was wrong only because I knew its alternative hypergeometric form. – Tito Piezas III Jun 07 '19 at 17:33
  • @DonAntonio: Kindly see my comment to J.G.'s answer why, when I use an integer relations algorithm, 8 correct decimal digits is simply not enough. – Tito Piezas III Jun 07 '19 at 17:54
  • 2
    Since it seems to be easy to overlook the implication of my comment, here is a practical tip: if you wrap your query with N[..., 100] in WolframAlpha, you get the correct approximation (at least this time!) – Kyle Miller Jun 07 '19 at 18:02
  • @KyleMiller: Thanks for the tip! Pls see my comment below on why I need more than 8 correct decimal digits. – Tito Piezas III Jun 07 '19 at 18:05

1 Answers1

1

The infinite series $\sum_{k\ge 1}a_k$ can be approximated by summing its first $n$ terms, but this may require very large $n$ for high accuracy. Since the $n$th term in $A$ is $O(1/n^4)$, the $n$th partial sum has a $O(1/n^3)$ error term. It therefore takes about $1000$ terms to get $9$ decimal places right. Or does it?

I don't know much about series acceleration of hypergeometric functions, or any methods WA might use to accelerate arbitrary series it didn't necessarily recognise add hypergeometric. But no general method accelerates all "logarithmically convergent" sequences, of which $A$ is an example. So go easy on WA.

J.G.
  • 115,835
  • Thanks for the explanation. I sometimes use WA to get 50 or more digits of integrals and infinite series, then use an integer relations algorithm to find closed-forms. It has worked many, many times. The important thing is these 50 digits must be accurate, or the algorithm will not find a relation. With your answer, I am left wondering for the times when the algorithm fails, if there is really no relation, or the digits inputted are merely wrong. – Tito Piezas III Jun 07 '19 at 17:43
  • 1
    Just for comparison, Maple seems to have no trouble evaluating the sum numerically to $100$ decimal places. – Robert Israel Jun 07 '19 at 17:45
  • 1
    @TitoPiezasIII I see your problem. You may have to write your own code to get accelerated expressions like $A$, once you've read a few acceleration techniques; that way, you can customise the precision. – J.G. Jun 07 '19 at 17:50
  • @RobertIsrael: Thanks for the comparison. That's why I called it a "bug", though I may have used the term loosely. If Maple has found a way, then the problem is a "bug" in the sense that it has a "fix" that is just waiting to be implemented. – Tito Piezas III Jun 07 '19 at 18:02