This is related to the question asked here, where the answer is that $\boldsymbol{X} = \mu + A\boldsymbol{Z}$. Note that $\boldsymbol{X}$ is the n-dimensional sample we seek, $\mu$ is the mean vector, $\Sigma = AA^T$ is the covariance matrix, and $\boldsymbol{Z}=(Z_1,\ldots,Z_n)^T$ is a vector of independent, standard normal variables. Essentially, the necessary pieces are $\mu, \Sigma,$ and $\boldsymbol{Z}$.
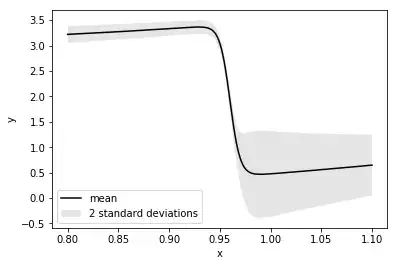
What I am wondering is: if we have only $\mu, \text{diag}(\Sigma),$ and $\boldsymbol{Z}$, is there any way to still draw a sample $\boldsymbol{X}$? Below is a very simple example, and I am wondering if there is a way to sample from this mean function with corresponding standard deviation.
import numpy as np
from matplotlib import pyplot as plt
def f(x):
"""arbitrary function"""
return 1.5*(1. - np.tanh(100.*(x-0.96))) + 1.5*x*(x-0.95) + 0.4 + 0.01*(1.-x)* np.random.random(x.shape)
X = np.linspace(0.8,1.1,1000)
# Observations and noise
y = f(X).ravel()
sigma = 0.2/y + 0.1*(1.-X)
plt.figure()
plt.plot(X, y, 'k-', label=u'mean')
plt.fill(np.concatenate([X, X[::-1]]),
np.concatenate([y - 2. * sigma,
(y + 2. * sigma)[::-1]]),
alpha=.1, fc='k', ec='None', label='2 standard deviations')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='lower left')
plt.show()