1

I am trying to write a program which calculates $\pi(x)$, however, the equation requires several instances of the letter $\rho$. I understand that $\rho$ indexes the non-trivial zeroes of the Riemann zeta function, but in the equation, there is no reference to an index of $\rho$, just $\rho$ itself. Please explain what value to give rho, or if it is supposed to somehow be integrated. Thank you.

$$\pi(x)=R(x)-\sum_\rho R\left(x^{\rho}\right)-\frac{1}{\text{ln } x}+\frac{1}{\pi}\text{ arctan }\frac{\pi }{\text{ln } x}$$

Steven Clark
  • 7,363
Jack Rothenberg
  • 23
  • 1
    It would be better if you would write out the equation and its context, but anyway, usually what's involved is a sum over the zeros of the zeta function, and the first few million of those have been tabulated – there's no simple formula for them (and indeed the most notorious open problem in Mathematics, the Riemann Hypothesis, is concerned with learning more about their location). – Gerry Myerson Jun 25 '19 at 02:40
  • 4
    Oh, and there are surely better ways to calculate $\pi(x)$ than to use any formula that needs the zeros of zeta. – Gerry Myerson Jun 25 '19 at 02:41
  • 1
    I can only guess as to which formula you saw, but $\rho$ probably indexes over the non-trivial zeros of the zeta function in canonical order (order of increasing magnitude for the origin). – dxdydz Jun 25 '19 at 02:43
  • 1
    I am guessing you are referring to the expression for $\psi_0(x)$ from the standard proof of the prime number theorem. They link to the tables of the zeta zeros compiled by Odlyzko. But then why not just use tables of prime numbers directly. – Conifold Jun 25 '19 at 02:46
  • What does rho mean when there is no index shown (ie. rho(3))? – Jack Rothenberg Jun 25 '19 at 02:50
  • @JackRothenberg The index is implied. The sum runs over the non-trivial zeroes of the zeta function in order of increasing magnitude, which can be indexed by the integers in an obvious way. – eyeballfrog Jun 25 '19 at 02:56
  • $\sum\limits_\rho f(\rho)$ is short-hand notation for $\sum\limits_{k=1}^\infty\left(f\left(\rho_k\right)+f\left(\rho_{-k}\right)\right)$ where $\rho_{-k}$ is the complex conjugate of $\rho_k$. The series is conditionally convergent where the sum over the non-trivial zeta zeroes must be taken in increasing order of the imaginary part. – Steven Clark Jun 25 '19 at 03:01
  • Welcome to MSE. Using this will make people happier: https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference I'll do a bit for you this time. Feel free to click "edit" on your question, to see what I changed. – it's a hire car baby Jun 25 '19 at 15:47
  • If you're still interested in your original formula rather than more efficient algorithms such as posted in the answer below, https://en.wikipedia.org/wiki/Prime-counting_function#Exact_form provides more insight into how your original formula is evaluated. – Steven Clark Jun 25 '19 at 17:06
  • Actual evaluations were considered here and here. – Raymond Manzoni Jun 25 '19 at 22:21
  • @GerryMyerson That sounds great, can you please give some examples? – Jack Rothenberg Jul 02 '19 at 02:14
  • I refer you to https://en.wikipedia.org/wiki/Prime-counting_function which mentions several good ways to count primes and gives links to more detailed descriptions, Jack. – Gerry Myerson Jul 02 '19 at 02:51

2 Answers2

1

Formula (1) for $\pi(x)$ below can be evaluated as illustrated in formula (2) below where $N\to\infty$ and $K\to\infty$.

(1) $\quad\pi(x)=R(x)-\sum\limits_\rho R\left(x^{\rho}\right)-\frac{1}{\text{ln } x}+\frac{1}{\pi}\text{ arctan }\frac{\pi }{\text{ln } x}$

(2) $\quad\pi(x)=\left(\sum\limits_{n=1}^N\frac{\mu(n)}{n}\left(\text{li}\left(x^{1/n}\right)-\sum\limits_{k=1}^K\left(\text{Ei}\left(\frac{\log(x)\rho_k}{n}\right)+\text{Ei}\left(\frac{\log(x)\rho_{-k}}{n}\right)\right)\right)\right)\\$ $\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad-\frac{1}{\log(x)}+\frac{1}{\pi}\tan^{-1}\left(\frac{\pi}{\log(x)}\right)\\$ $\qquad\qquad\ \ =\left(\sum\limits_{n=1}^N\frac{\mu(n)}{n}\left(\text{li}\left(x^{1/n}\right)-2\,\Re\left(\sum\limits_{k=1}^K\text{Ei}\left(\frac{\log(x)\rho_k}{n}\right)\right)\right)\right)-\frac{1}{\log(x)}+\frac{1}{\pi}\tan^{-1}\left(\frac{\pi}{\log(x)}\right)$

The following figure illustrates formula (2) above for $\pi(x)$ in orange overlaid on the reference function $\pi(x)$ in blue where formula (2) is evaluated at $N=10$ and $K=200$. I'm a bit skeptical with respect to the convergence of formulas (1) and (2) above for $\pi(x)$ at small values of $x>1$.

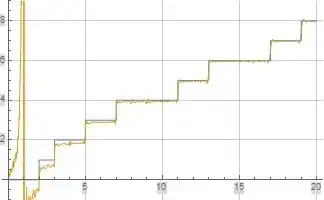
Illustration of Formula (2)

Figure (1): Illustration of Formula (2) for $\pi(x)$ evaluated at $N=10$ and $K=200$ (orange curve)

Steven Clark
  • 7,363
0

You could just do the this - it must be much more efficient:

def primes(N):
  p = range(2,N+1)
  n = 2
  while n*n <= N:
    p = [x for x in p if (x % n) or x <= n]
    n = n + 1
  return p

def pi(N):
  return len(primes(N))
David C. Ullrich
  • 89,985