10

Now also asked on MathOverflow and answered affirmatively there.

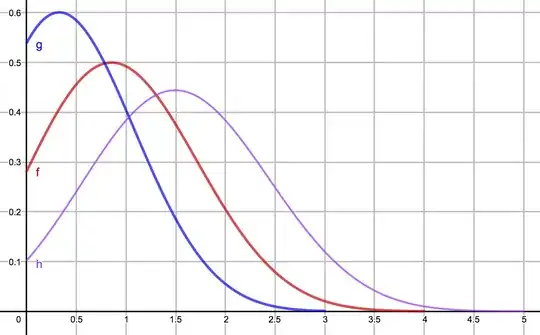
Let there be $n$ pairs of shoes in a box. The the probability that from the $r \le n$ shoes I am taking out of the box there are exactly $p$ pairs is given by \begin{equation*} \mathbb{P}_{n}^{(r)}(p) = \frac{\binom{n}{p} \binom{n-p}{r-2p} 2^{r-2p}}{\binom{2n}{r}}. \end{equation*} For $n = 15$ and $r \in \{6,8,10\}$. The function (assuming the continuous factorial equivalents) looks like this: enter image description here

I am interested in finding the area under that curve, namely $$\int_{0}^{\frac{r}{2}} \frac{\binom{n}{p} \binom{n-p}{r-2p} 2^{r-2p}}{\binom{2n}{r}} \ \text{d}p$$ According to numerical estimates in the comments I suspect that it converges to 1 for $n = r \to \infty$.

I consulted this question but could derive how that would help me.

I also thought about writing the first product of binomial coefficients as $$ \binom{n}{n - p}\binom{n - p}{r - 2p} $$ which is similar to the form $\binom{f(x)}{f(y)} \binom{f(y)}{f(x)}$ mentioned in this question.

ViktorStein
  • 4,838
  • Seems not: $(1,1): 0.4593\dots$, $(2,2): 0.7220\dots$, $(3,3): 0.8580\dots$, and the integral for $n = r$ appears to monotonically increase for larger $n$. It's around $1 - 10^{-6}$ for $n = 20$. – Eric Towers Jun 28 '19 at 17:58
  • 1
    In other words, we want to show that $$\int_0^{\frac{n}{2}}\frac{1}{4^p\left(n-2p\right)!\left(p!\right)^2},dp\sim\frac{\left(2n\right)!}{2^n\left(n!\right)^3},$$ or using Stirling's approximation, $$\int_0^{\frac{n}{2}}\frac{1}{4^pp^{2p+1}(n-2p)^{n-2p+\frac12}},dp\sim\frac{2\sqrt\pi}n\left(\frac{2}n\right)^n.$$ – ə̷̶̸͇̘̜́̍͗̂̄︣͟ Jul 01 '19 at 08:37

0 Answers0