Inequalities involving square roots.

Question

I was trying to solve the following inequation: $$ x^2≤16 \Rightarrow x≤\sqrt{16} \Rightarrow x≤4 \text{ and } x≤-4 $$ But the solution given in my textbook is [-4,4], which is only possible when $x≥-4$ and $x≤4$. What have I done wrong?

(Sorry I could not format my question properly, I am new to this site.)

You have to be very careful with the inequality signs! I think you just put one $\leq$ wrong, you should have put $\geq$. — Matti P., Jul 19 '19 at 11:20

score 1 · Answer 1 · edited Jul 19 '19 at 14:36

1

$$ x^2\leq 16 \Rightarrow |x|\leq \sqrt{16} \Rightarrow -4\leq x\leq 4 $$ The plot may help:

edited Jul 19 '19 at 14:36

vonbrand

27,812

answered Jul 19 '19 at 11:47

A.G.

2,781

score 0 · Answer 2 · answered Jul 19 '19 at 11:21

0

Write $$x^2\le 16$$ as $$(x-4)(x+4)\le 0$$

answered Jul 19 '19 at 11:21

Dr. Sonnhard Graubner

95,283

I tried solving it that way just now, I am getting x≤-4 and x≤4. I think I have done something wrong. – Jul 19 '19 at 11:29
No it is $$-4\le x\le 4$$ the solution set. – Dr. Sonnhard Graubner Jul 19 '19 at 11:32
So x≥-4, and I can't understand how is it so. – Jul 19 '19 at 11:34
A product of two factors is negative, if one factor is negative and the other one positive. – Dr. Sonnhard Graubner Jul 19 '19 at 11:36
Taking the square root on both sides we get $$|x| \le 4$$ – Dr. Sonnhard Graubner Jul 19 '19 at 11:38
So $$x\le 4$$ or $$-x\le 4$$ – Dr. Sonnhard Graubner Jul 19 '19 at 11:40

score 0 · Answer 3 · answered Jul 19 '19 at 11:34

Consider the inequality $$ f(x) = x^2 - 16 \leq 0 $$

A fool-proof way of always getting the inequality equations correct is the following: Start with the equality (instead of inequality) equation. In this case, it's $$ x^2 - 16 =0 \qquad \Rightarrow \qquad x \in \left\{ -4, 4 \right\} $$ The second step is to divide the real number line at these points. We have two points of division (two solutions), so we have to divide the number line into three parts. Now consider each of the part's sign individually.

First part is $x<-4$. What is the value of the expression ($f(x)$) in this area? We can plug in for example $x=-5$ and see that the answer is $f(-5) = 9>0$. Therefore, the expression is positive in this part of the number line.
Second part is $-4 \leq x \leq 4$. We can plug in for example $f(0) = -16<0$. The expression is negative in this part.
Third part is $x>4$. We can again plug in some test value, let's say $f(5) = 9>0$. In this part, the function is positive

Looking at the three sections, we see that the only part where $f(x)$ was negative was the second part. Therefore the answer is $$ -4 \leq x \leq 4 $$

score 0 · Answer 4 · 2019-07-19T11:49:31.730

Take $x=-5$, which verifies $x\le-4$, doesn't it ?

But $x^2=25>16$ !

What you did wrong is to consider that

$$a^2\le b^2\implies a\le b$$ whatever $a,b$. This is not true when $b$ is negative !

A trick:

An inequation such as $f(x)\le0$ where $f$ is a continuous function is true in intervals that are delimited by the roots ($f(x)=0$), because by continuity you cannot change the sign without crossing zero.

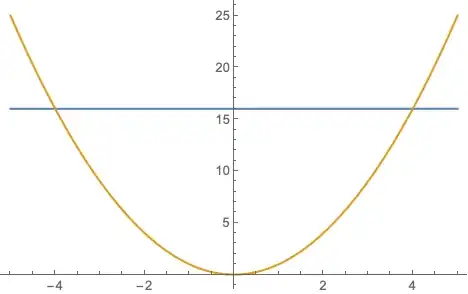
The roots of your equation $x^2-16=0$ are $x=-4$ and $x=4$. They partition the real line in three intervals (ignoring the roots themselves),

$$(-\infty,-4),(-4,4),(4,\infty).$$

The solution set is made of the union of some of these intervals. You can pick a single value in each and check if they fulfill the inequation. E.g.

$$f(-5)=9>0,\\f(0)=-16<0,\\f(5)=9>0.$$

Now you should know where the solutions reside.

score 0 · Answer 5 · answered Jul 19 '19 at 11:48

0

It may be less confusing to use $|x|$, which is non-negative:

$$ |x|^2=x^2≤16 \implies |x|≤\sqrt{16}=4 \implies -4\le x≤4 $$

answered Jul 19 '19 at 11:48

J. W. Tanner

60,406

Inequalities involving square roots.

5 Answers5