The integral $\int\limits_0^\infty\frac{x^4e^x}{(e^x-1)^2} \mathrm{d}x$

Question

How to calculate the following integral $$\int_0^\infty\frac{x^4e^x}{(e^x-1)^2}\mathrm{d}x$$ I would like to solve this integral by means of two different ways: for example, integration by parts and using Residue Theorem.

Answer 1

I will generalise this integral to solve $$I_n=\int_0^\infty\frac{x^ne^x}{(e^x-1)^2}\mathrm{d}x$$ Applying integration by parts and L'Hôpital's rule gives $$\begin{align} I_n &=\left[-\frac{x^n}{e^x-1}\right]_0^\infty+n\int_0^\infty\frac{x^{n-1}}{e^x-1}\mathrm{d}x\\ &=n\int_0^\infty\frac{x^{n-1}}{e^x-1}\mathrm{d}x\\ &=n\,\zeta(n)\,\Gamma(n)\\ &=\zeta(n)\,\Gamma(n+1)\\ \end{align}$$ where $\Re{(n)}\gt1$. The last equality follows from the famous Bose integral (See proofs at 1, 2 and 3). The answer required is then given by $$I_4=\zeta(4)\,\Gamma(5)=\frac{\pi^4}{90}\cdot4!=\frac{4\pi^4}{15}$$

Answer 2

Using $$ \frac1{(1-x)^2}=\sum_{n=0}^\infty(n+1)x^n $$ \begin{eqnarray} \int_0^\infty\frac{x^4e^x}{(e^x-1)^2}\mathrm{d}x&=&\int_0^\infty\frac{x^4e^{-x}}{(1-e^{-x})^2}\mathrm{d}x\\ &=&\int_0^\infty x^4e^{-x}\sum_{n=0}^\infty(n+1)e^{-nx}\mathrm{d}x\\ &=&\sum_{n=0}^\infty\int_0^\infty(n+1)x^4e^{-(n+1)x}\mathrm{d}x\\ &=&\sum_{n=0}^\infty \frac{24}{(n+1)^4}\\ &=&24\zeta(4)\\ &=&\frac{4\pi^4}{15}. \end{eqnarray}

Answer 3

$$I=\int_0^\infty\frac{x^4e^x}{(e^x-1)^2}\ dx\overset{e^{-x}=y}{=}\int_0^1\frac{\ln^4x}{(1-x)^2}\ dx=\sum_{n=1}^\infty n\int_0^1x^{n-1}\ln^4x\ dx=\sum_{n=1}^\infty\frac{4!}{n^4}=4!\zeta(4)$$

Answer 4

The computation of the given integral becomes in one step (partial integration) $\displaystyle \int_0^\infty\frac {x^4e^x}{(e^x-1)^2}\; dx=- \int_0^\infty x^4\left(\frac 1{e^x-1}\right)'\; dx =\color{blue}{4J_-(4)}$ with the notations $$ J_\pm(s) = \int_0^\infty x^{s-1}\cdot\frac 1{e^x\pm1}\; dx \ , $$ and $J_-(4)$ is directly related to https://en.wikipedia.org/wiki/Riemann_zeta_function#Definition.

Instead of using the known special values of the zeta function, here is an explicit calculation using the Residue Theorem.

---

Let $f_s$ (with $s=2,4,6,8\dots$ for our Eulerian purposes) be the function $$ f_s(z)=\frac{z^{s-1}}{e^z-1}\ , $$ defined on the complex plane without the obvious poles of the denominator. (Note that $0$ is a removable singularity in the cases of interest.) The computational idea for $J_+(4)$ comes after the substition $x=2y$ in $$ \begin{aligned} J_-(4) &=2^3 \int_0^\infty y^3\cdot\frac 2{e^{2y}-1}\; dy \\ &=8 \int_0^\infty y^3\left(\frac 1{e^y-1}-\frac 1{e^y+1}\right)\; dy \qquad\color{red}{(*)} \\ &=8J_-(4)-8J_+(4)\ , \\[2mm] &\qquad\qquad\text{ and in this spirit we get} \\[2mm] 1\cdot J_-(2) &= 2\cdot J_+(2) \\ 7\cdot J_-(4) &= 8\cdot J_+(4) \\ 31\cdot J_-(6) &= 32\cdot J_+(6) \end{aligned} $$ and so on.

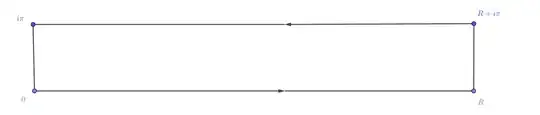
Fix now some $R>0$, and consider the rectangle contour $C(R)$ with corners, in order, $0,R,R+i\pi,i\pi$:

The integral of $f_4$ on $C(R)$ vanishes by the Residue Theorem. We let now $R\to+\infty$.

• The integral of $f_4$ from $0$ to $R$ converges to $J_-(4)$, the integral we need.

• The integral of $f_4$ from $R$ to $R+i\pi $ converges to $0$, because of the exponential term in the denominator.

• The integral of $f_4$ from $R+i\pi$ to $i\pi$ converges to $$ \begin{aligned} -\int_0^\infty(x+i\pi)^3\cdot \frac 1{e^{x+i\pi}-1}\; dx &=\int_0^\infty(x+i\pi)^3\cdot \frac 1{e^x+1}\; dx \\ &=J_+(4)-3\pi^2\; J_+(2)\text{ modulo }i\Bbb R\ . \end{aligned} $$

• The integral of $f_4$ on the segment $[0,i\pi]$ must be computed, for a general even $s>0$ we can work similarly: $$ \begin{aligned} \int_{i\pi}^0 z^3 \cdot \frac 1{e^z-1}\; dz &= -\int_0^\pi i^3t^3\cdot \frac1{(\cos t-1)+i\sin t}\; d(it) \text{ with }z=it \\ &= \int_0^\pi it^3 \cdot\frac1{2i\sin(t/2)\;(\cos (t/2)+i\sin(t/2))}\; i\; dt \\ &= \int_0^\pi it^3\cdot\frac{\cos (t/2)-i\sin(t/2)}{2\sin(t/2)}\; dt \\ &= \int_0^\pi \frac 12 t^3\; dt \text{ modulo }i\Bbb R\ . \\ \end{aligned} $$

---

Using the above method, we reduce the computation of $J\pm(4)$ to the one of $J_\pm(2)$. It may be useful to write explicitly the relation obtained by using the Residue Theorem for some more values. (We need only the relations for $2$ and $4$.) $$ \begin{aligned} 0 &= J_-(2) + 0 \underbrace{-\int_0^\infty x\cdot\frac 1{-(e^x+1)}\; dx} _{=J_+(2) } -\int_0^\pi\frac 12\cdot t\; dt \\ 0 &= J_-(4) + 0 \underbrace{-\int_0^\infty \text{Real}((x+i\pi)^3)\cdot\frac 1{-(e^x+1)}\; dx} _{=J_+(4)-3\pi^2 J_+(2)} +\int_0^\pi\frac 12\cdot t^3\; dt \\ 0 &= J_-(6) + 0 \underbrace{-\int_0^\infty \text{Real}((x+i\pi)^5)\cdot\frac 1{-(e^x+1)}\; dx} _{=J_+(6)-10\pi^2 J_+(4) +5\pi^4J_+(2)} -\int_0^\pi\frac 12\cdot t^5\; dt \end{aligned} $$ and so on.

This gives rise to $$ \begin{aligned} +\frac 1{2\cdot 2}\pi^2 &= J_-(2) +[\ J_+(2)\ ]\ , \\ -\frac 1{2\cdot 4}\pi^4 &= J_-(4) +[\ J_+(4)-3\pi^2J_+(2)\ ]\ , \\ +\frac 1{2\cdot 6}\pi^6 &= J_-(6) +[\ J_+(6)-10\pi^2J_+(4)+5\pi^4 J_+(2)\ ]\ , \\ -\frac 1{2\cdot 8}\pi^8 &= J_-(8) +[\ J_+(6)-21\pi^2 J_+(6) + 35\pi^4 J_+(4)-7\pi^6J_+(2)\ ]\ , \end{aligned} $$ and so on. (In the pattern, the coefficients are binomial coefficients, appearing in the terms of the binomial expansion of $(x+i\pi)$ to the power $1,3,5,7$ and so on.)

---

We are now in position to compute the integral in the OP, and also check: $$ \zeta(s)=\frac 1{\Gamma(s)}\int_0^\infty \frac{x^{s-1}}{e^x-1}\; dx = \frac 1{\Gamma(s)}J_-(s) $$ for some first eulerian values of $s$ (namely two, four, six, ...)

• The first line above gives $\frac 14\pi^2=\frac{1+2}2J_-(2)$, so $J_-(2) =\frac 16\pi^2$. Because $\Gamma(2)=1!=1$, this gives a proof of $\zeta(2)=\frac 1{1!}J_-(2)=\frac 16\pi^2$.

• The second line gives the value for $J_-(4)+J_+(4)=\frac{7+8}8 J_-(4)$ as $3\pi^2 J_+(2)-\frac 1{2\cdot 4}\pi^4 =\pi^4\left( 3\cdot\frac 12\cdot \frac 16-\frac 18\right)=\frac 18\pi^4$, so $$ J_-(4)= \frac 1{15}\pi^4\ . $$ Because $\Gamma(4)=3!=6$, this gives a proof of $\zeta(4)=\frac 1{3!}J_-(4)=\frac 1{90}\pi^4$.

This also answers the OP, the integral to be comupted is $$ \color{blue}{ \boxed{\qquad 4J_-(4)=\frac 4{15}\pi^4\ . \qquad}} $$

• Let us compute also $J_-(6)$. The third line gives the equality of $J_-(6)+J_+(6)=\frac{31+32}{32}J_-(6)$ and $\left(\frac 1{2\cdot 6}+10\cdot\frac 78\cdot\frac 1{15}-5\cdot\frac 12\cdot\frac 16\right)\pi^6 =\frac {1+7-5}{12}\pi^6=\frac 14\pi^6$. This gives $J_-(6)=\frac {32}{63}\cdot\frac 14\pi^6=\frac 8{63}\pi^6$. This is also a check of $\zeta(6)$ being $\frac 1{5!}\cdot \frac 8{63}\pi^6=\frac 1{945}\pi^6$.

---

Note: All computations were done explicitly, no details were omitted. This makes the answer long, too long, but the computational idea is already clear from the position $\color{red}{(*)}$, when the contour to be used is known.