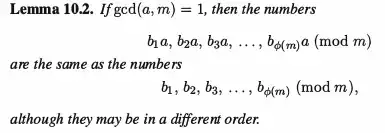2

First i want to talk about my motivation for this theorem and how i came up with this proof. In modular arithmetic, we have the group $U(n)$ closed under modular multiplication and by Euler's Theorem we know that,

$$a^\varphi \equiv_n 1$$

for $\forall a \in U(n)$. IFF this theorem is true, we know that order of $\forall a \in U(n)$ divides the order of the group it is in, i.e for some integer $Q$,

$$\varphi = Q\cdot|a|.$$

I observed that a similar property also holds true for the finite groups $S_{n}$ and $D_{2n}$. So i concluded that we can generalize this theorem to all finite groups, so that we would never be have to prove a variance of the same theorem.

Euler's Generalized Theorem: For $\forall g \in G$, $|g|$ divides $|G|$ where $(G, \cdot)$ is a finite group. Consequently $g^{|G|} = e$.

So by this motivation, i examined proof of the Euler's Theorem for $U(n)$ and looked up if i can generalize this proof. And i have seen that whole proof depends on the lemma,

Lemma 10.2

So we can generalize the lemma as follows:

If $a \in G$ (i.e. satisfies the properties which holds true for all elements of $G$, like $(a, n) = 1$ for $a \in U(n)$), then the sets formed by sequences,

$$p_1, p_2, ..., p_i, ..., p_{|G|}$$

and $$ap_1, ap_2, ..., ap_i, ..., ap_{|G|}$$ (where $p_i$ is each element of $G$) are the same.

Here goes my proof:

Lets assume that if we multiply $a$ with $p_j$ and $p_k$ (where $j \ne k$), we obtain the same result $c$ because it is the only case which the theorem above can fail. Since otherwise all results would be distinct and there would be exactly $|G|$ results which are all in the $G$ because of the closure property.

$$ap_j = c$$ $$ap_k = c$$

So, it follows that, $ap_j = ap_k$. If we multiply each side with the inverse of $a$ from left (since the group may not be Abelian):

$$p_j = p_k$$

Which contradicts with our assumption. So that the lemma have to be true. Q.E.D.

Lets proceed to the proof for main theorem.

Since the sequences above are the same, their multiplication is also the same.

$$\prod_i^{|G|} p_i = a^{|G|} \cdot \prod_i^{|G|} p_i $$

It follows that $$a^{|G|} = 1$$ and so $\forall a \in G$, $|a|$ divides $|G|$, which completes my proof.

the_fox
  • 5,805
İbrahim İpek
  • 1,126
  • 1
    You might be interested to know that this property holds more generally: Lagrange's theorem guarantees that if $H$ is a (not necessarily cyclic) subgroup of the finite group $G$, then $|H|$ divides $|G|$. – the_fox Jul 20 '19 at 17:29
  • See also https://math.stackexchange.com/questions/28332/is-lagranges-theorem-the-most-basic-result-in-finite-group-theory – lhf Jul 20 '19 at 21:14

1 Answers1

3

Your proof almost works, but unfortunately it falls just short.

The reason it doesn't work is the equality of products you wrote : in fact the sequences are not the same; they have the same elements but possibly (and in fact almost all the tim) not in the same order.

So if $G$ is not commutative, i.e. if the order in which you multiply matters (this is the case for $S_n$ and $D_{2n}$ ), then you can't equate the two products.

So your proof works if $G$ is a commutative group.

However, the result is correct, even if the group is not commutative, the proof will simply have to be different. It is a corollary of Lagrange's theorem, you may want to look that up if you're interested.

Maxime Ramzi
  • 43,598
  • 3
  • 29
  • 104