There are a few interesting finite sums of digamma of a rational argument listed on Wikipedia (from this paper). One of them is the following:
$$\sum _{m=1}^{N-1}\psi \left({\frac {m}{N}}\right)\cdot {\frac {m}{N}}=-{\frac {\gamma }{2}}(N-1)-{\frac {N}{2}}\log N-{\frac {\pi }{2}}\sum _{m=1}^{N-1}{\frac {m}{N}}\cdot \cot {\frac {\pi m}{N}}$$
I found a related sum with Mathematica, using numerical experiments (linear fit actually helped):
$$\sum _{m=1}^{2N-1}(-1)^m \frac {m}{2N} \left[ \psi \left(\frac {m}{2N}\right)+\frac {\pi }{2} \cot \frac {\pi m}{2N} \right] =\frac {\gamma }{2}+ N \log 2$$
I still would like to prove this, and the linked paper could probably help, but it's quite long and complicated, so if anyone has better ideas, I'd like to hear them.
I suppose we can use:
$$\pi z \cot \pi z=\sum _{n=0}^{\infty } \left(\frac{z}{n+z}-\frac{z}{n-z}\right)-1$$
$$z \psi (z)=-\gamma z +\sum _{n=0}^{\infty }\left({\frac {z}{n+1}}-{\frac {z}{n+z}}\right)$$
I wanted this formula because of the method of exhaustion, referenced in this question:
$$\int_0^1f(x)\,dx=-\sum_{n=1}^\infty\sum_{m=1}^{2^n-1}\frac{(-1)^m}{2^n}f\left(\frac m{2^n}\right)$$
Though I'm far from finished with the original proof I needed it for, I found an interesting consequence:
$$\frac{1}{2} \log (2 \pi)=-\sum _{n=1}^\infty \sum _{m=1}^{2^n-1} \frac{(-1)^m m }{2^n} \left(\frac{1}{2^n} \left( \frac{ \pi}{2} \cot \left(\frac{\pi m}{2^n}\right)+\gamma \right)+\log (2)\right)$$
Since:
$$-\int_0^1 u \psi(u) du=\frac{1}{2} \log (2 \pi)$$
As an additional question, the odd sum also appears to be approximately linear, so if anyone has ideas:
$$\sum _{m=1}^{2N}(-1)^m \frac {m}{2N+1} \left[ \psi \left(\frac {m}{2N+1}\right)-\frac {\pi }{2} \cot \frac {\pi m}{2N+1} \right] -\frac {\gamma }{2}= ?$$
Turns out, there's a more general relation for digammas of rational arguments ($m<N$) (see Wikipedia):
$$\psi \left({\frac {m}{N}}\right)=-\gamma -\log (2N)-\frac {\pi }{2} \cot \left(\frac {\pi m }{N}\right)+2\sum _{n=1}^{\left\lfloor {\frac {N-1}{2}}\right\rfloor }\cos \left({\frac {2\pi n m}{N}}\right)\ln \sin \left({\frac {\pi n}{N}}\right)$$
Which clearly can be used to derive more finite sums. However, it's quite complicated, so I haven't yet managed to derive my result.
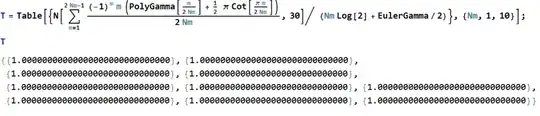
\left(\frac{m}{2 N}\right)\right)=\frac{N}{m}+\frac{1}{2} \pi
\cot \left(\frac{\pi m}{2 N}\right)$$ $$\sum _{m=1}^{2 N-1} \frac{(-1)^m m \left(\psi \left(1+\frac{m}{2 N}
\right)+\psi \left(1-\frac{m}{2 N}\right)\right)}{4 N}+\frac{1}{2}=N
\log (2)+\frac{\gamma}{2}$$ – stocha Jul 29 '19 at 10:14
$$g(x)=\begin{cases} \frac{x^b-x^a}{1-x} &\mbox{if } 0<x<1 \ 0 & \mbox{if } x> 1 \end{cases} $$
and $\Re s>-\Re a,-\Re b$.
– stocha Jun 28 '21 at 21:22