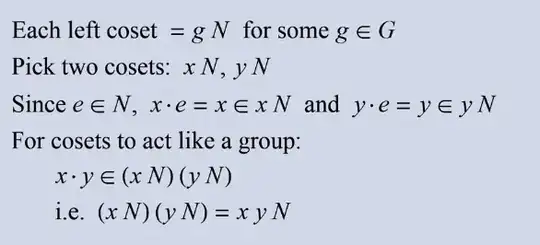I'm watching this video on quotient groups and came across the following(you don't have to click the link):
$G$ is a group and $N$ is its subgroup.
Using $N$ to make cosets : $N, g_1N, g_2N, g_3N, \ldots$
I get why $x\in xN$ and $y\in yN$, but I'm not able to figure out the last two lines. Any help understanding why they say $x\cdot y \in (xN)(yN)$ for cosets to act like a group? It is obvious right? (Since $x\in xN$ and $y\in yN$, it is obvious $x\cdot y \in (xN)(yN)$. I don't get how this makes the cosets a group...)