Show that the series $\sum_{n>0} \frac{(-1)^n}{n}\left \lfloor \frac{\ln n}{\ln 2} \right \rfloor$ converges

Question

Show that the series $$\sum_{n>0} \frac{(-1)^n}{n}\left \lfloor \frac{\ln n}{\ln 2} \right \rfloor$$ converges, where $\left \lfloor x \right \rfloor$ is the integer part of $x$.

I have used the fact that

$\ln n\rightarrow\sum_{k=1}^{n} \frac{1}{k} $

but its difficult to express the integer part of this sum.

Using the hint in the answer, I need to show that :

1. $a_n=\frac{1}{n} \left \lfloor \frac{ln(n)}{ln(2)} \right \rfloor$ have a constant signe
2. $a_n \rightarrow 0$ and decreasing .

The first point is obvious because $\frac{ln(n)}{n} \rightarrow 0$

I have to show that $a_{n+1}<a_{n}$ to apply the alternative series test i am stuck here

Answer 1

For this sum, Alternating Series Test is not directly applicable because the magnitudes of the summands do not decay monotonely:

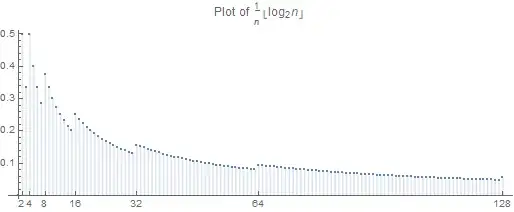
For the proof, it is convenient to group terms according to the value of $\lfloor \log_2 n\rfloor$. Indeed, for each given $N$, we may write

$$ \sum_{n=1}^{N} \frac{(-1)^n}{n} \lfloor \log_2 n \rfloor = \sum_{n=1}^{N} \sum_{m=1}^{\infty} \frac{(-1)^n}{n} \cdot m \mathbf{1}_{\{ 2^m \leq n < 2^{m+1} \}} = \sum_{m=1}^{\infty} A_{N,m}, \tag{1} $$

where $A_{N,m}$ is defined by

$$ A_{N,m} = m \sum_{\substack{n \leq N \\ 2^m \leq n < 2^{m+1}}} \frac{(-1)^n}{n}. $$

Now we refer to the following intermediate observation in the proof of Alternating Series Test:

Lemma. Let $(a_k)_{m \leq k \leq n}$ be a sequence of non-negative and non-increasing real numbers. Then

$$ \left| \sum_{m \leq k \leq n} (-1)^k a_k \right| \leq a_m. $$

From this, we immediately find that

$$|A_{N,m}| \leq \frac{m}{2^m} \quad \text{for all} \quad N, m \geq 1. $$

Since this bound is summable in $m$, meaning that $\sum_{m\geq 1} m/2^m < \infty$, Weierstrass $M$-test shows that the sum in $\text{(1)}$ converges as $N\to\infty$. Moreover, the limit can be computed by taking limit term-wise:

$$ \lim_{N\to\infty} \sum_{n=1}^{N} \frac{(-1)^n}{n} \lfloor \log_2 n \rfloor = \sum_{m=1}^{\infty} \lim_{N\to\infty} A_{N,m}. $$

Answer 2

Consider the terms from $n=2^m$ to $2^{m+1}-1$. There are $2^m$ of these, and for each the integer part is $m$.

Therefore the sum over these is

$m\sum_{k=0}^{2^m-1}(-1)^k/(2^m+k)\\ =m\sum_{k=0}^{2^{m-1}-1}(1/(2^m+2k)-1/(2^m+2k+1))\\ =m\sum_{k=0}^{2^{m-1}-1}(1/((2^m+2k) (2^m+2k+1)))\\ \lt m\sum_{k=0}^{2^{m-1}-1}(1/((2^m) (2^m)))\\ =\dfrac{m}{2^{m+1}} $

and the sum of these converges.

Answer 3

The series restricted to $[2^m,2^{m+1}-1]$ equals $$ m\sum_{n=2^m}^{2^{m+1}-1}\frac{(-1)^n}{n}=m\left[\sum_{n=2^m}^{2^{m+1}-1}-\frac{1}{n}+\sum_{\substack{n\in[2^m,2^{m+1}-1]\\n\text{ even}}}\frac{2}{n}\right] $$ or $$ m\left[-H_{2^{m+1}-1}+2H_{2^m-1}-H_{2^{m-1}-1}\right]= m\left[-H_{2^{m+1}}+2H_{2^m}-H_{2^{m-1}}+\frac{1}{2^{m+1}}-\frac{2}{2^m}+\frac{1}{2^{m-1}}\right]. $$ Since $$ H_N = \log N+\gamma +\frac{1}{2N}+O\left(\frac{1}{N^2}\right) $$ we have $$ m\sum_{n=2^m}^{2^{m+1}-1}\frac{(-1)^n}{n} = m\left[\frac{1}{2^{m+2}}+O\left(\frac{1}{4^m}\right)\right] $$ and the original series is convergent by comparison with $\sum_{m\geq 0}\frac{m}{2^{m+2}}$.