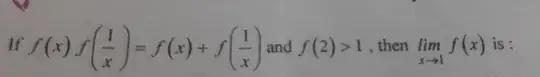1

If $f(x) f(1/x) = f(x) + f(1/x)$ and $f(2) > 1$, then $\lim_{x \to 1} f(x)$ is:

Original image

My professor told me to use the squeeze theorem whenever we are to find the limit of an unknown function. I don't think that it will be applicable here as no desire information is given here. Then how to find a limit in this question?

Kais Hasan
  • 607
B Luthra
  • 205

2 Answers2

1

Suppose $f:\mathbb{R}^+\rightarrow\mathbb{R}$ (otherwise just set $f(x)=2$ for $x\leq 0$). If $f$ is not continuous, it may happen that the limit does not exist. To see why this is true, take $$f(x)=\begin{cases}c, &\text{ if }x>1\\ \frac{c}{c-1}, &\text{ if }x<1\\0,&\text{ if } x=1\end{cases}$$ with $c>1$.

If we suppose that $f$ is indeed continuous, it is not hard to see that there is no positive $x$, such that $f(x)=1$. This, combined with the fact that $f(2)>1$, gives $f(x)>1$ for all positive $x$. This gives $f(1)=2$ and so $$\lim_{x\rightarrow 1}f(x)=f(1)=2$$

L3435
  • 547
0

Note that $(f(x)-1)(f(1/x)-1)=1$. So if we guess $f(x)=x^n+1$ then $((x^n+1)-1)((\frac{1}{x^n}+1)-1)$ which equals 1 so our guess was correct. Therefore, $f(2)=2^n+1>1$ which is true for all $n$. So the limit is simply equal to 2.

Akshat Sharma
  • 476
  • I understand you made a good guess for the function, but that doesn't mean that $2$ is the limit for all possible functions with the given property. It's possible the limit doesn't exist. – Rushabh Mehta Oct 23 '19 at 16:07
  • There's no need to 'guess', it can be proved easily. But the restriction is $f(x)$ must be a polynomial. – Zenix Oct 23 '19 at 16:08
  • My answer is definitely not a rigorous one. Perhaps it's more qualified as a comment. – Akshat Sharma Oct 23 '19 at 16:13
  • 1
    I don't think it's fair to discourage Akshat by giving him a down vote. His solution is partly correct. (+1) from me – Zenix Oct 23 '19 at 16:14