1

$$ \lim_{x\to +\infty} x\left(\frac{\pi}{4} - \arctan\left(\frac{x}{x+1}\right)\right) $$

I tried to do this with some kind of substitution but failed miserably. Any hints or help?

Blue
  • 75,673
MathematicianBalkaniad
  • 11

4 Answers4

4

Substitute $y:=\frac{1}{x+1}$ to rewrite your limit as$$\lim_{y\to0}(1-y)\frac{(\arctan 1-\arctan(1-y))}{y}=\lim_{y\to0}(1-y)\cdot\arctan^\prime1=\frac12.$$Or if we take @DinnoKoluh's approach,$$\arctan1-\arctan\frac{x}{x+1}=\arctan\frac{1}{2x+1}\approx\frac{1}{2x}.$$

J.G.
  • 115,835
  • Wow, how did you know to make y that in the substitution? – MathematicianBalkaniad Nov 06 '19 at 18:29
  • @MathematicianBalkaniad Since $\frac{\pi}{4}=\arctan 1$, I wanted the other arctangent's argument to be in the form $1-y$. – J.G. Nov 06 '19 at 18:30
  • I am a little confused in how you got the derivative though. Isnt the formula the other way around? The answer would be the same but negative? – MathematicianBalkaniad Nov 06 '19 at 20:08
  • @MathematicianBalkaniad $f^\prime(a)=\lim_{y\to0}\frac{f(a)-f(a-y)}{y}$ is just as correct as $f^\prime(a)=\lim_{y\to0}\frac{f(a+y)-f(a)}{y}$ (proof is an exercise). – J.G. Nov 06 '19 at 20:10
2

Hint: $$ \arctan(x)\pm\arctan(y) = \arctan(z) $$ where $z$ is: $$ z = \frac{x\pm y}{1\mp xy} $$ And knowing the fact that: $$ \lim_{x\to0} \frac{\arctan(f(x))}{f(x)} = 1 $$ If $ f(x) = 0 $ as $x\to0$.

This can be proven by the L'Hospital's rule: $$ \lim_{x\to0} \frac{\arctan(f(x))}{f(x)} = \lim_{x\to0} \frac{\frac{1}{1+f^2(x)}f'(x)}{f'(x)} = \lim_{x\to0} \frac{1}{1+f^2(x)} = 1. $$

Dinno Koluh
  • 753
1

First set $1/x=h$

using my answer here in Inverse trigonometric function identity doubt: $\tan^{-1}x+\tan^{-1}y =-\pi+\tan^{-1}\left(\frac{x+y}{1-xy}\right)$, when $x<0$, $y<0$, and $xy>1$,

$$\arctan 1-\arctan\dfrac x{x+1}=\arctan1-\arctan\dfrac1{h+1}=\cdots=\arctan\dfrac h{2+h}$$

$$ \lim_{x\to +\infty} x\left(\frac{\pi}{4} - \arctan\left(\frac{x}{x+1}\right)\right) =\lim_{h\to0^+}\dfrac{\arctan\dfrac h{2+h}}{\dfrac h{2+h}}\cdot\lim_{h\to0^+}\dfrac1{2+h}=?$$

lab bhattacharjee
  • 274,582
1

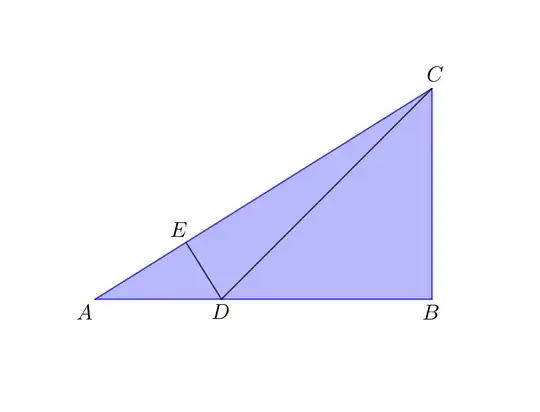I nice approach using triangles. Use the following figure, where $\triangle ABC$ is right-angled with $\overline{BC} = x>0$ and $\overline{AB} = 1+x$. Take $D$ on $AB$ so that $\overline{AD} = 1$ and $E$ on $AC$ so that $DE\perp AC$. enter image description here By definition $$\angle CAB = \arctan\left(\frac{x}{x+1}\right),$$ and by the External Angle Theorem $$\angle ACD = \frac{\pi}4-\angle CAB.$$ Note that $\overline{AC} = \sqrt{2x^2+2x+1}$, and use the fact that $\triangle ADE \sim \triangle ABC$ to conclude that $$\overline{DE} = \frac{x}{\sqrt{2x^2+2x+1}},$$ and $$\overline{AE} = \frac{x+1}{\sqrt{2x^2+2x+1}},$$ so that $$\overline{CE} = \frac{2x^2+x}{\sqrt{2x^2+2x+1}},$$ and $$\angle ACD = \arctan\frac{\overline{DE}}{\overline{CE}}=\arctan\left(\frac{1}{2x+1}\right).$$ So, as per the other answers, your limit is equal to $$\lim_{x\to +\infty} x\arctan\left(\frac1{2x+1}\right) = \frac12.$$

dfnu
  • 7,528