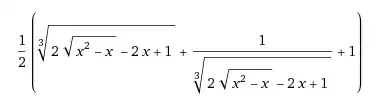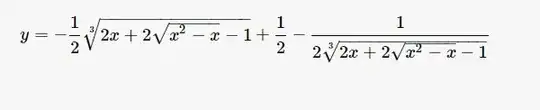3

I want to get the inverse of aforementioned function. I know it is not one-to-one normally, but my $x$ is restricted to $[0,1]$ where we have no problem. I didn't really know how to inverse such a complicated function so I tried to get an answer online.

I visited 2 different websites, wolframalpha and emathhelp. My problem is, these 2 "calculators" give me a slightly different result and I can't find out if it is the same or not, so I don't know what the correct inverse is.

I post 2 pictures with the 2 results. The first is from wolfram and the second for emath.

enter image description here

enter image description here

I've noticed that if I insert the $-1$ in the cubic root by writing it as $\sqrt[3]{-1}$ the signs of $2x$ and $1$ change accordingly, but the sign of the square root is staying the same.

Perhaps I somehow transform the $\sqrt[3]{-1}$ into a complex number involving $i$ and that affects the sign of the square root ? Not sure.

Any help would be greatly appreciated.

EDIT: My question seems to be the same with another and thank you for pointing it out to me. However people in the comments pointed out that for $ x$ in $[0,1]$ the term inside the square root becomes negative. Is that a problem? Can I accept this solution as the inverse function in the restricted domain $[0,1]$? I would still like a more detailed answer about the actual inverse of the function if this isn't the correct one, if of course someone can offer it. Thanks a lot .

Thomas
  • 477
  • 1
    The question turned out to be a duplicate, so I delete my answer. In case you still want to review the example cubic, it is here. – Jyrki Lahtonen Nov 12 '19 at 17:06
  • Thanks for the link and for the help. I still havent understood however. Is the first function given by Claude with the $i$ and the roots, the inverse of my function? It still has a square root with a negative term inside, given $x \in [0,1]$. I'd really appreciate an answer on that. – Thomas Nov 12 '19 at 18:10

2 Answers2

4

In fact, it is a bit more complex. You face a cubic equation in $x$ $$2x^3-3x^2+y=0$$

Solving for $x$, you should get for the branch you consider $$x=\frac 12+\frac{\left(1+i \sqrt{3}\right)}{4} \sqrt[3]{2 \sqrt{y^2-y}+2 y-1}+\frac{(1-i \sqrt{3})}{4 \sqrt[3]{2 \sqrt{y^2-y}+2 y-1}}$$ which is real.

If you use the trigonometric method, you will see (after simplifications) that $$x=\frac{1}{2}-\sin \left(\frac{1}{3} \sin ^{-1}(1-2 y)\right)$$

Claude Leibovici
  • 260,315
  • 2
    [+1] Good point, Claude : the trigonometric method (https://math.stackexchange.com/q/1908861) often provides simpler results – Jean Marie Nov 11 '19 at 11:35
  • Thanks for the answer. However, im not sure i understood. Is $\frac{1}{2}-\sin \left(\frac{1}{3} \sin ^{-1}(1-2 y)\right)$ also the inverse function of $2x^3-3x^2$? Also, what is the "branch" you mention ? – Thomas Nov 11 '19 at 16:02
  • @Thomas. Yes for the first question. For the second, there are three real roots for the equations in the considered ranges. – Claude Leibovici Nov 12 '19 at 04:58
  • Thanks. Regarding the negative term in the square root for $x \in [0,1]$, does that mean that the first function you mentioned can't be the inverse? – Thomas Nov 12 '19 at 09:18
1

If by [0,1] you mean the numbers 1 and 0 then the square root is of no interest to you and can be left out, in both cases its result is 0, its just that wolfram and emathhelp tried to solve for a general inverse.

Andrej
  • 51
  • I mean that my $x \in [0,1]$. Yeah I figured that the websites didn't take this into consideration. However the square root is $0$ when $x$ is $0$ or $1$. What about all the in between numbers – Thomas Nov 11 '19 at 10:50
  • The inverse function has multiple solutions on the interval (0,1), so you can't write that out as an equation of the form y = x but instead it would have to be some y^2 = x, wolfram chose to leave out one set to make it y = x – Andrej Nov 11 '19 at 10:59
  • Not exactly sure what you mean. Are both of the answer I got correct? – Thomas Nov 11 '19 at 11:01
  • Both are correct but the cubic roots are redundant to your [0,1] case – Andrej Nov 11 '19 at 11:08