1

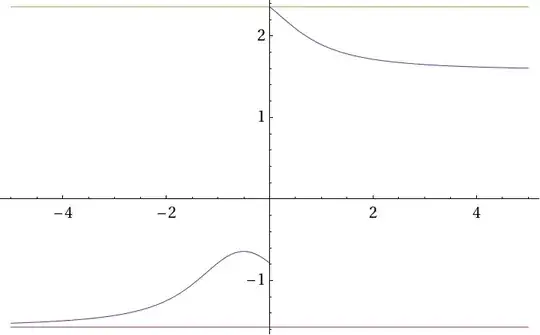
It is given $f:\mathbb R \rightarrow \mathbb R$ $$f(x):=\tan^{-1}(x+1)+ \cot^{-1}(x)$$ $\mathcal R_f=?$

So far, I've learned $\tan$ and $\cot$ are complementary functions, therefore $$\tan^{-1}(x) + \cot^{-1}(x)=\frac{\pi}{2}.$$

I entered a loop using $$\tan(x) =\frac{1}{\cot(x)}\;.$$

Can I use $\tan$ for the whole expression and from there on use the $\tan$ addition formula?

Is there a way of finding the image without using derivatives and limits?

Blue
  • 75,673
PinkyWay
  • 4,565

2 Answers2

2

Hint Combine the complementarity identity in the question with the arctangent addition identity $$\arctan u \pm \arctan v = \arctan\frac{u \pm v}{1 \mp uv} \pmod \pi .$$ (I'm not sure that this approach avoids limits in the strict sense, since finding the range of the resulting function requires knowing about the asymptotic behavior of $\arctan$.)

Travis Willse
  • 99,363
  • this formula turned out to be very useful. At the very end we get: $$f(x)=\frac{\pi}{2};+;\tan^{-1}\Big(\frac{1}{x^2+x+1}\Big)$$ The expression in the denominator is always (strictly) positive so, in order to get the maximum value of $f(x)$, I used the $y_0$ value of the vertex of the parabola by the formula instead of derivative. The result is: $$f(\mathbb R)=\Big\langle\frac{\pi}{2}, \frac{\pi}{2};+;\tan^{-1}\Big(\frac{4}{3}\Big)\Big\rangle$$ – PinkyWay Nov 13 '19 at 13:45
  • Great, this looks mostly correct. I'm not familiar with the $\langle \cdots \rangle$ notation in this context, but $f(\Bbb R)$ includes $f\left(-\frac{1}{2}\right) = \frac{\pi}{2} + \arctan \frac{4}{3})$, but not $\frac{\pi}{2}$, so the range is half-open: Using the complementarity identity we can rewrite $$f(x) = \frac{\pi}{2} + \arctan(x + 1) - \arctan x ,$$ but $\arctan$ is strictly increasing, so $\arctan(x + 1) - \arctan x$ is positive for all $x$, and thus $f(x) > \frac{\pi}{2}$ for all $x$. – Travis Willse Nov 13 '19 at 17:33
  • Also, note that $\arctan \frac{4}{3}$ can be written as $2 \arctan \frac{1}{2}$; cf. my expression for $f\left(-\frac{1}{2}\right)$ a comment under Mani's answer. – Travis Willse Nov 13 '19 at 17:34
  • I forgot other countries use '(' & ')' for open intervals. I see what's wrong. I didn't include the $\arctan\Big(\frac{4}{3}\Big)$. If the product $;uv;>;1,$ and the sign in the denominator changes, there are two cases: either $u,v;> 0$ or $u,v;< 0$, which means $\tan$ is either postive or negative. When proving the statement we add or subtract $\pi$, I have to prove $\arctan\notin \Big(-\frac{\pi}{2},\frac{\pi}{2}\Big)$ which matters in the restriction? – PinkyWay Nov 13 '19 at 19:43
  • Hm, I'm not sure quite what your question is, but yes, the upper endpoint of the interval is in the range. (In any case, the denominator does not vanish in our particular case.) Which country uses $\langle a, b \rangle$ for an open interval? – Travis Willse Nov 13 '19 at 19:51
  • Well, I come from Croatia and I know for sure most of the Eastern European countries. I hadn't known for the other notations before my friends went to study in Austria and Germany. – PinkyWay Nov 13 '19 at 19:54
  • I thought if this $uv>1$ and $uv<1$ is only if the $\arctan{u}$ and $\arctan{v}$ aren't complementary, so the restriction doesn't allow that. – PinkyWay Nov 14 '19 at 09:02
  • I'm not sure quite what you mean by "the restriction doesn't allow that", but see https://math.stackexchange.com/questions/1724348/what-is-arctanx-arctany – Travis Willse Nov 18 '19 at 09:12
0

Note that $\cot^{-1}(\pm \infty)= 0$ and $\tan^{-1} (\pm \infty) =\pm \pi/2$, $\cot^{-1}(0^+)= \pi/2$ so the least value taken by the given function $$f(x)= \cot^{-1}x +\tan^{-1} (1+x)$$ is $-\pi/2$. its (global) maximum value will occur at $x=0$ which is $f(0)=\pi/2+\pi/4= 3\pi/4.$ Sot the range of the given function is $(-\pi/2, 3\pi/4]$

See the attached figure where $f(0)=3\pi/4=2.3561...$. The upper horizontal line depicts this value and the lower horizontal line depicts the lower bound of $-\pi/2.$

enter image description here

Mani khurana
  • 46
  • The claims about the location of the maximum and the value of the maximum are both incorrect. The maximum occurs at $x = -\frac{1}{2}$ (in fact, the function is symmetric about the line that equation defines), and the maximum value is $\frac{\pi}{2} + 2 \arctan \frac{1}{2} = 2.49809\ldots$. – Travis Willse Nov 13 '19 at 07:41
  • It's true that some authors define $\operatorname{arccot}$ with a discontinuity at $0$, but OP's assertion of the identity $\arctan x + \operatorname{arccot} x = \frac{\pi}{2}$ means that they are not using such a convention. – Travis Willse Nov 13 '19 at 08:42
  • (Also, the numerical approximation cannot be right, since $\frac{3 \pi}{4} < \pi = 3.14159\ldots$.) – Travis Willse Nov 13 '19 at 08:44
  • Oh! sorry I meant $f(0)=3\pi/4=2.3561$, this is also the global maximum of $f(x)$, At $x=-1/2$, there is a local maximum not the global one. I have corrected the the value of $f(0$ in my edit. – Mani khurana Nov 13 '19 at 08:57
  • Again, your claim that the global maximum occurs at $x = 0$ and not $x = -\frac{1}{2}$ relies on a convention for $\operatorname{arccot}$ that OP's question makes clear is not the one they are using; rearranging the identity in the question statement we can take OP's definition to be $\operatorname{arccot} x = \frac{\pi}{2} - \arctan x$). Using OP's convention, the function does not have a jump discontinuity, and the (global) maximum occurs at $x = -\frac{1}{2}$ as mentioned above. – Travis Willse Nov 13 '19 at 17:47