Prove that $\frac{a+b}{2}≥\sqrt{ab}$

Question

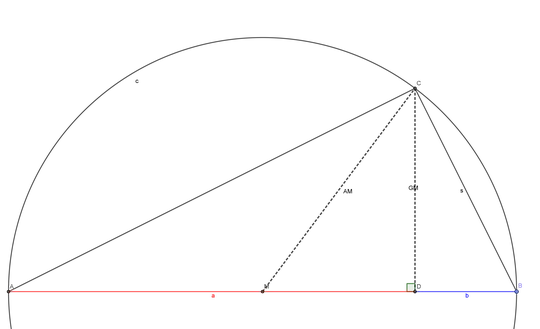
I'm working on a proof of AM-GM inequality, but for now I would like to prove more basic propositions.

Prove that the arithmetic-geometric mean inequality holds for lists of numbers of length $2$. In other words, prove that for all positive real numbers $a$ and $b$ $$\frac{a+b}{2}≥\sqrt{ab}$$

My attempt:

We know that $(a-b)^2 ≥ 0 $

Expanding

$$a^2 - 2ab + b^2 ≥ 0$$

Adding $4ab$ to both sides

$$a^2 + 2ab + b^2 ≥ 4ab \implies $$ $$(a+b)^2 ≥ 4ab \implies $$ $$a+b ≥ 2\sqrt{ab} \implies $$ $$\frac{a+b}{2} ≥ \sqrt{ab}$$

$\Box$

Is it correct?

Answer 1

This proof is correct, but the usual approach is even simpler: rearrange $\frac12(\sqrt{a}-\sqrt{b})^2\ge0$.

Answer 2

For the sake of completeness I am adding a well known geometric proof of this inequality:

Combining the cathetus theorem ($s^2=b(a+b)$) and Pythagoras' theorem we get: $GM=\sqrt{b(a+b)-b^2}=\sqrt{ab}$.

And since the diameter $a+b$ of the circle c is twice the radius, we get: $AM=radius=\frac{a+b}{2}$

Answer 3

The OP's proof is perfect. Let's have another.

Let

$$ m\,:=\,\frac{a+b}2 $$ and $$ d\,:=\,\frac{a-b}2 $$ so that $$ a\,=\,m+d\qquad\mbox{and}\qquad b\,=\,m-d $$ hence

$$ \sqrt{a\cdot b}\,=\,\sqrt{(m+d)\cdot(m-d)}\,=\,\sqrt{m^2-d^2} \,\le\,m\,=\,\frac{a+b}2 $$

Great!

Remark: $$ \frac{a+b}2=\sqrt{a\cdot b}\quad\Leftrightarrow\quad d=0 $$ i.e. $$ \frac{a+b}2=\sqrt{a\cdot b}\quad\Leftrightarrow\quad a=b $$