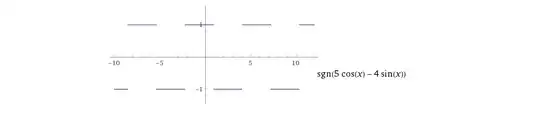
Find $\dfrac{dy}{dx}$ if $y=\sin^{-1}\bigg[\dfrac{5\sin x+4\cos x}{\sqrt{41}}\bigg]$
My Attempt
Put $\cos\theta=5/\sqrt{41}\implies\sin\theta=4/\sqrt{41}$ $$ y=\sin^{-1}\big[\sin(x+\theta)\big]\implies\sin y=\sin(x+\theta)\\ y=n\pi+(-1)^n(x+\theta)\\ \boxed{\frac{dy}{dx}=(-1)^n} $$
But my reference gives the solution $y'=1$, am I missing something here ?
As you correctly pointed out we have
$$y = \arcsin\left[\sin\left(x +\theta\right) \right],$$ where $\theta = \arcsin\frac4{\sqrt{41}}$.
Now observe that ($k\in \Bbb Z$) $$ \arcsin\sin \alpha = \begin{cases}\alpha-2k\pi & \left(2k\pi-\frac{\pi}2\leq \alpha < 2k\pi+\frac{\pi}2\right)\\ - \alpha - (2k-1)\pi & \left(2k\pi+\frac{\pi}2\leq \alpha < 2k\pi+\frac{3\pi}2\right).\end{cases} $$
Thus your function is the triangular wave (see Figure below)
$$ y = \begin{cases} x +\theta- 2k \pi & \left(2k\pi-\frac{\pi}2-\theta\leq x < 2k\pi+\frac{\pi}2-\theta\right)\\ -x-\theta-(2k-1)\pi-\theta & \left(2k\pi+\frac{\pi}2-\theta\leq x< 2k\pi+\frac{3\pi}2-\theta\right) \end{cases} $$
whose derivative is
$$
y =
\begin{cases}
1 & \left(2k\pi-\frac{\pi}2-\theta< x < 2k\pi+\frac{\pi}2-\theta\right)\\
-1 & \left(2k\pi+\frac{\pi}2-\theta< x<2 k\pi+\frac{3\pi}2-\theta\right)
\end{cases}
$$
I think your reference is wrong.
$y'=1$ is true half the time - the other half $y'=-1$ as you wrote.
Rewriting,
$$\sin y=\dfrac{5\sin x+4\cos x}{\sqrt{41}}=\sin(x+\theta)\tag 1$$
with $\theta=\tan^{-1}\frac4{5}$ and recognize $y\in[-\frac\pi2,\frac\pi2]$, hence $\cos y \ge 0$,
$$\cos y= \text{sgn}[\cos(x+\theta) ]\cos(x+\theta) $$
Take the derivative of (1),
$$\> y' = \dfrac{\cos(x+\theta)}{\cos y} = \dfrac{\cos(x+\theta)}{\text{sgn}[\cos(x+\theta) ]\cos(x+\theta)} \\ =\text{sgn}[\cos(x+\theta) ]= \begin{cases} 1, & x+\theta -2k\pi \in \left(-\frac{\pi}2,\frac{\pi}2\right]\\ -1, & x+\theta -2k\pi\in \left(\frac{\pi}2,\frac{3\pi}2\right] \end{cases} $$
which, as seen in the graph below, alternates at either -1 or 1 depending on the value of $x$.
