We have burgers equation $U_t+UU_x=0$.
We set the following initial conditions:
- $U(x,0) = 1 + 2/\pi \cdot \arctan(x) $
with clamped endpoints
- $U_\text{right endpoint}=0$
- $U_\text{left endpoint}=2$
Solving using the finite difference method with Forward Euler gives the following plot over time.
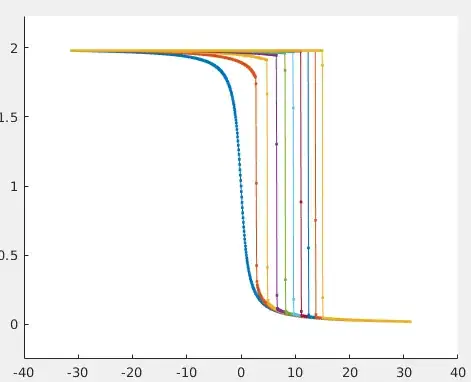
We have that the solution becomes 'square' and/or discontinuous over time. I am wondering what could explain this behavior. I believe it has to do with the top of the wave traveling faster than the bottom of the wave. However, this seems unsatisfactory.