Given three chords on a circle which form an interior triangle what is the area of the triangle formed?

Question

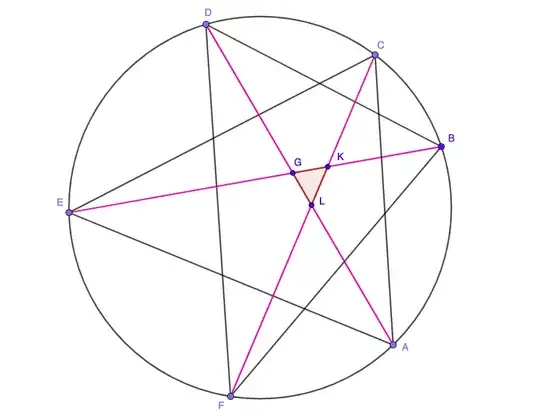
Using an argument similar to this one, the probability of a triangle being formed is $\frac{1}{15}$ since the number of ways six points on the circumference of a circle can be grouped into three sets of two is $\frac{6!}{2!^33!}=15$ and only one of these ways to group forms a triangle. Another way to think about this is forming all chords from six points and looking at $\triangle GKL$, the interior triangle formed.

Given a triangle is formed by three chords of a circle, what is the area of the triangle in terms of the location of the six points on the circle? I am looking run a simulation of the expected area given three random chords but having a hard time simply solving for the area of the triangle.

For simplicity I think we can assume that the circle is a unit circle of radius one?

Answer 1

While I think it is probably possible to compute the expected area exactly, it hardly seems worthwhile. We can choose $6$ angles uniformly between $0$ and $2\pi$ and order them so that $$0\leq \theta_0 < \theta_i < \cdots < \theta_5 < 2\pi$$ WLOG we can take $\theta_0=0.$ Then the expected value is $$\frac{1}{32\pi^5}\int_0^{2\pi}\mathrm{d}\theta_1 \int_{\theta_1}^{2\pi}\mathrm{d}\theta_2 \int_{\theta_2}^{2\pi}\mathrm{d}\theta_3 \int_{\theta_3}^{2\pi}\mathrm{d}\theta_4 \int_{\theta_4}^{2\pi}A(\theta_1,\theta_2,\theta_3,\theta_4,\theta_5)\mathrm{d}\theta_5 $$ where $A$ is a rational function of sines and cosines. Presumably this can be integrated in closed form by making the Weierstrass substitution on each of $\theta_5, \theta_4, \dots$ in turn. I shudder at the thought, but maybe a CAS can do it.

Following Βασίλης's lead, I wrote a simulation, using a circle of radius $1$. I consistently get a value around $.083.$ The code is given below. I just used Βασίλης's formulas, without checking them. You ought to do that, as well as checking my code for errors. I used the understanding I made in the comments. If the angles are $\theta_0, \theta_1, \dots, \theta_5$ in cyclic order, then the chords connect $\theta_i$ and $\theta_{i+3}$ for $i=1,2,3.$

from math import sin, cos, pi, sqrt
from random import random
import numpy as np

trials = 100000

def area():
    theta = sorted(2*pi*random() for _ in range(6))
    A = [sin(theta[i]) - sin(theta[i+3]) for i in range(3)]
    B = [cos(theta[i+3]) - cos(theta[i]) for i in range(3)]
    C = [-sin(theta[i])*B[i]-cos(theta[i])*A[i] for i in range(3)]
    D = [A[i]*B[(i+1)%3]-A[(i+1)%3]*B[i] for i in range(3)]
    Dx = [-B[i]*C[(i+1)%3]+B[(i+1)%3]*C[i] for i in range(3)]
    Dy = [-A[i]*C[(i+1)%3]+A[(i+1)%3]*C[i] for i in range(3)]
    x = [Dx[i]/D[i] for i in range(3)]
    y =  [Dy[i]/D[i] for i in range(3)]
    M = np.ones((3,3))
    M[0,:] = x
    M[1,:] = y
    return .5*abs(np.linalg.det(M))

total = 0
squares = 0
for _ in range(trials):
    a = area()
    total += a
    squares += a*a
mean = total/trials
var = squares/trials - mean*mean
print(f'{trials} trials')
print(f'Mean: {mean}') 
print(f'Std deviation {sqrt(var)}')

Typical output:

100000 trials
Mean: 0.08274184243163976
Std deviation 0.12692829789994378

Answer 2

An analytic approach:

The six points you have at hand form three lines with equations (supposing they form a triangle, this is indeed true):

$$\begin{align} A_1x+B_1y+C_1&=0,\\ A_2x+B_2y+C_2&=0,\\ A_3x+B_3y+C_3&=0, \end{align}$$

where $|A_i|+|B_i|>0$. Now, solving the following systems (all do have a unique solution since the three lines form a triangle and, hence, intersect pairwise each other):

$$S_1=\left\{\begin{array}{l} A_ix+B_iy+C_i=0,\\ A_jx+B_jy+C_j=0\end{array}\right., $$ where $j=i+1\mod3$ and $i=1,2,3$. Let $X_1,X_2,X_3$ be these points with cordinates:

$$x_i=\frac{D_i^x}{D_i},y_i=\frac{D_i^y}{D_i},$$

where $D_i=A_iB_j-A_jB_i$, $D_i^x=-B_iC_j+B_jC_i$ and $D_i^y=-A_iC_j+A_jC_i$, with $i=1,2,3$ and $j$ as above.

Now that you have the triangle's endpoints, it is easy to find its area e.g. using the determinant formula: $$E=\frac{1}{2}\left|\vec{X_1X_2},\vec{X_2X_3}\right|$$