2

I'm currently reading Turaev's book "Quantum invariants..." and I'm struggling with the following definition on page 62.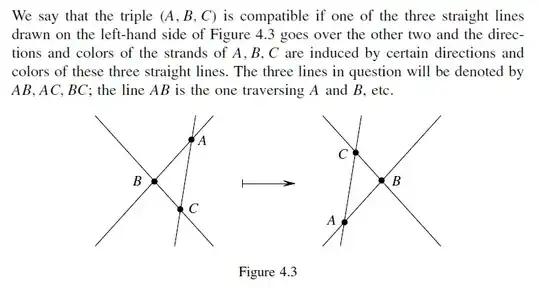enter image description here

Where $A,B,C$ is one of the following crossings (up to isotopy)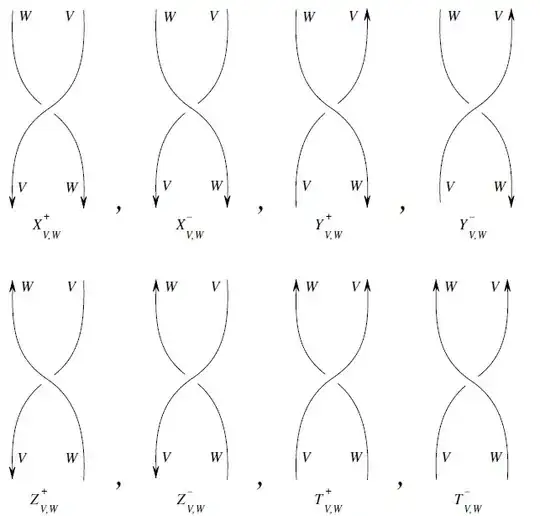enter image description here

representing morpisms in a ribbon category and $V,W$ are objects of a strict monoidal category. By coloring a strand we mean that we assign an object of the monoidal category to the strand, as in the picture of the crossings where the colors are $V$ and $W$.

Can someone please provide me with an example of what a compatible triple is and what isn't and why?

Amontillado
  • 1,179

1 Answers1

1

Here is my understanding. I am a beginner and it could be wrong. If you want triple (A,B,C) to be compatible, it should satisfies 2 conditions. One is the directions and colors of three stright lines should be induced by directions and colors of A,B, and C. and it should be 'compactible'. For example, $(A,B,C)=(X^+_{V,W}, X^-_{V,U}, X^+_{W,U})$ statisfies this condition, but $(A,B,C)=(Y^-_{V,W}, X^-_{V,U}, X^+_{W,U})$ do not. Becaues the stright line $AB$ in the later one do not have a well-defined direction. And something like $(X^+_{V,W}, X^-_{V,U}, X^+_{K,L})$ also does not satisfy this condition.

The second one is, after replacing the crossing point A, B, and C by what they stand for (i.e. $X^\pm_{U,V}, Y^\pm_{U,V}, Z^\pm_{U,V}, T^\pm_{U,V}$), one of these line ($AB,AC,$ or $BC$) should be above the other two lines. So than you can actually make this move $\Omega_3$ legelly. For example, $(X^+_{V,W}, X^-_{V,U}, X^+_{W,U})$ does not satisfy this condition, while $(X^+_{V,W}, X^-_{V,U}, X^-_{W,U})$ and $(X^+_{V,W}, X^+_{V,U}, X^+_{W,U})$ do.

likeeatingoctopus
  • 444