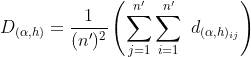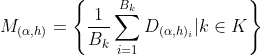Is it possible to convert output of an equation in an unordered set?

Question

I am total novice in algebra, so I need help regarding what I try to do... I have built the following equation:

$M[B_{k}]_{(\alpha ,h)} = \frac{1}{B_{k}}\sum_{i=1}^{B_{k}}\left [ \frac{1}{(n')^2}\left ( \sum_{j=1}^{n'}\sum_{i=1}^{n'}\left ( \sqrt{\sum_{i=1}^{n}\left ( rec_{h_{i}}-rec_{\alpha_{i}} \right )^2} \right )_{ij} \right ) \right ]_{i}$

and these three statements:

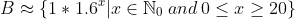
$B\approx \left \{ 1*1.6^x | x \in \mathbb{N}_{0} \: and\: 0\leq x\geq 20 \right \}$

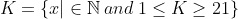
$K=\left \{ x|\in \mathbb{N}\:and \: 1\leq K\geq21 \right \}$

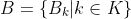
$B = \left \{ B_{k}| k\in K \right \}$

Here is what is the process I tried to describe:

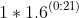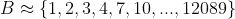
B is a family set of length 21, containing rounded values of $1 * 1.6^{(0:21)}$ looking like $B \approx \left \{1,2,3,4,7,10,...,12089 \right \}$

K is an index set (of B) looking like that: 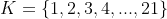$K = \left \{1,2,3,4,...,21 \right \}$

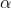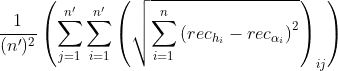
$M[B_{k}]_{(\alpha ,h)}$ is the mean of means (if k = 1 only, if not see further) of euclidian distances calculated on variables n between n' records of $\alpha$ and h (both randomly sampled in a dataset) ; if I made no mistakes it is done by this part of the equation: $\frac{1}{(n')^2}\left ( \sum_{j=1}^{n'}\sum_{i=1}^{n'}\left ( \sqrt{\sum_{i=1}^{n}\left ( rec_{h_{i}}-rec_{\alpha_{i}} \right )^2} \right )_{ij} \right )$

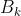This part: $M[B_{k}]_{(\alpha ,h)} = \frac{1}{B_{k}}\sum_{i=1}^{B_{k}}\left [...\right ]_{i}$ aims to tel that the operation done in the brackets [...] is bootstraped $B_{k}$ times and mean of the output is calculated to obtain finally mean of means of means (if k > 1 ).

Could you please tell me if this logics sounds good ?

And finally, if I want to considere $M[B_{k}]_{(\alpha ,h)}$ as a familly set containing all results from bootstrap, I am OK to write that :

$M_{(\alpha ,h)} = \left \{ \frac{1}{B_{k}}\sum_{i=1}^{B_{k}}\left [ \frac{1}{(n')^2}\left ( \sum_{j=1}^{n'}\sum_{i=1}^{n'}\left ( \sqrt{\sum_{i=1}^{n}\left ( rec_{h_{i}}-rec_{\alpha_{i}} \right )^2} \right )_{ij} \right ) \right ]_{i}\right \}$

One of the question I did not manage to answer is, if e.g. *k = 3, the output is only the one computed with 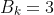$B_{k} = 3$ or is it $B_{k} = 1 + B_{k} = 2 + B_{k} = 3$ (which is not what I have done in R...).

The other question is that the output of this computation will certainly not be ordered (values may not be crescent) ; is it a problem ?

Many thanks for your help, and $Merry \: \: Christmas !$

Can you explain why you want to pack this fairly complex algorithm into one single algebraic expression ? It would be clearer if you wrote a separate expression for each step - which you have started to do in your explanation anyway. — gandalf61, Dec 25 '19 at 11:59
That's a damn good question ! Mainly because I am unskilled in maths... And I tryied to summary the process (which was pretty hard to me ;)). Please feel free to suggest any improvements or to spot mistakes !! — RPO, Dec 25 '19 at 16:25

RPO · Answer 1 · 2019-12-26T11:13:55.150

Following @gandalf61 recommandations, I propose the same process in separated steps:

I set these three statements:

$B\approx \left \{ 1*1.6^x | x \in \mathbb{N}_{0} \: and\: 0\leq x\geq 20 \right \}$

$K=\left \{ x|\in \mathbb{N}\:and \: 1\leq K\geq21 \right \}$

$B = \left \{ B_{k}| k\in K \right \}$

B is a family set of length 21, containing rounded values of $1 * 1.6^{(0:21)}$ looking like $B \approx \left \{1,2,3,4,7,10,...,12089 \right \}$ . Values in this set are the quantity of iteration to do on the whole process (at the begining input records are randomly sampled, and at the end we compute the mean of the total number of iteration, so the mean of B=1 to B=12089).

K is an index set (of B) looking like that: $K = \left \{1,2,3,4,...,21 \right \}$

The whole described process aims at computing mean distance between n' records of $\alpha$ and n' records of h which are in the begining randomly sampled (in a big dataset); this operation is bootstraped B times and mean of the B times output have to be calculated. n are dimensions number (quantitive variables), whose values are used to calculate Euclidean distances

So first Euclidean distance d is calculated between record $\alpha$ and record h:

$d_{(\alpha ,h)}=\sqrt{\sum_{i=1}^{n}\left(rec_{h_{i}}-rec_{\alpha_{i}}\right)^2}\right$

Then Mean Euclidean D distance is calculated between all n' records of $\alpha$ and h:

$D_{(\alpha ,h)} = \frac{1}{(n')^2}\left ( \sum_{j=1}^{n'}\sum_{i=1}^{n'}\ d_{(\alpha ,h)_{ij}} \right )$

These steps have to be bootstraped B times; and outputs of each B times have to be stored in a vector/set(?). So, I think that there is a mistake here in my equation in this process. E.g. I need to store result for B = 1 (k = 1) ; B = 7 (k = 5), etc. to assess effect of iterations increase on results linearity (but I don't need to store results of B = 1 + B = 2 + ... + B = 12089)

Here is what I propose to explain this part of the process. Could you tell me if I am right? I wonder if I can built results of M like that because outputs of bootstraps B may not be ordered as it is means (of means of means), e.g. M(B = 7) > M(B = 12089) is totally possible.

$M_{(\alpha ,h)} = \left \{ \frac{1}{B_{k}}\sum_{i=1}^{B_{k}}D_{(\alpha ,h)_{i}} | k\in K\right \}$

Many thanks for your help !

Is it possible to convert output of an equation in an unordered set?

1 Answers1