How would one compute the following improper integral:
$$\int_0^\infty \sin\left(\frac{1}{x^2}\right) \, \operatorname{d}\!x$$
without any knowledge of Fresnel equations?
I was thinking of using the comparison theorem since $\sin x$ is never greater than 1. However, I can't find a function always greater than 1 between 0 and infinity such that its integral from 0 to infinity converges.
Thanks.
By "Fresnel equations," I assume you mean stuff like
$$\mathcal{F}(z) = \int_0^z dt \: e^{i \frac{\pi}{2} t^2}$$
Have no fear: I will produce everything from scratch without reference to anyone named Fresnel. That said, I will produce integrals with quadratic phase, but I will show you how to deal with them.
Begin with a substitution $u=1/x^2$:
$$\begin{align}\int_0^{\infty} dx \: \sin{\left ( \frac{1}{x^2}\right)} &= \frac{1}{2} \underbrace{\int_0^{\infty} du \: u^{-3/2} \, \sin{u}}_{\text{integrate by parts}} \\ &= \frac{1}{2} \underbrace{\left [ -2 u^{-1/2} \sin{u} \right]_0^{\infty}}_{\text{this is zero}} + \underbrace{\int_0^{\infty} du \: u^{-1/2} \, \cos{u}}_{u=v^2}\\ &= 2 \int_{0}^{\infty} dv \: \cos{v^2} \\ &= \Re{\left[\int_{-\infty}^{\infty} dv \: e^{i v^2} \right ]} \end{align}$$
Now, let's focus on this last integral. It is far from obvious that this even converges; I will show below that it does. I hope you are familiar with Cauchy's integral theorem, though.
Consider the integral in the complex plane
$$\oint_C dz \: e^{-z^2}$$
where $C$ is the following contour:
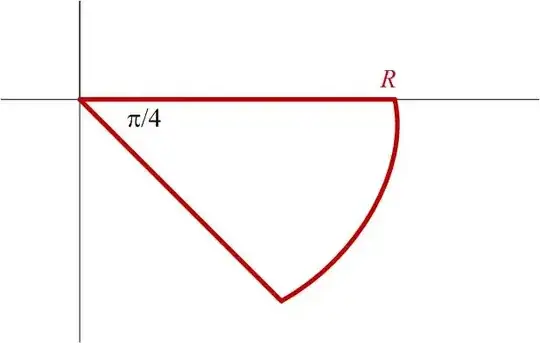
That is, a $45^{\circ}$ wedge of radius $R$, where we will set $R \rightarrow \infty$. Because there are no poles inside the contour, the above integral is zero. We then write the integral around this contour as
$$\oint_C dz \: e^{-z^2}=\int_0^R dx \: e^{-x^2} + R \int_0^{-\pi/4} d\theta \: e^{-R^2 \cos{2 \theta}} e^{-i R^2 \sin{2 \theta}} + e^{-i \pi/4} \int_R^0 dv \: e^{i v^2}=0$$
I hope you see that the second integral, that about the arc, vanishes as $R \rightarrow \infty$. It vanishes because of the exponential term in the integrand which vanishes very quickly in this limit. Because this integral vanishes, we are then left with the following relation:
$$\int_0^{\infty} dx \: e^{-x^2} - e^{-i \pi/4} \int_0^{\infty} dv \: e^{i v^2} = 0$$
Thus
$$\int_0^{\infty} dv \: e^{i v^2} = e^{i \pi/4} \int_0^{\infty} dx \: e^{-x^2} $$
Using the fact that the integral on the RHS is equal to $\sqrt{\pi}$ and that we are only interested in the real part of the integral on the LHS, we finally get
$$\int_0^{\infty} dx \: \sin{\left ( \frac{1}{x^2}\right)} = \sqrt{\frac{\pi}{2}}$$
A related problem. Recalling the Mellin transform
$$ F(s) = \int_{0}^{\infty} x^{s-1} f(x) dx. $$ We are going to relate our integral to the above integral. Using the change of variables $x=\frac{1}{y}$ to the integral in consideration gives
$$ \int_0^\infty \sin\left(\frac{1}{x^2}\right) \, \operatorname{d}\!x = \int_0^\infty \frac{\sin\left(y^2\right) }{y^2}\, \operatorname{d}\!y. $$
Following it with another change of variables $y=\sqrt{u}$ yields
$$ \int_0^\infty \frac{\sin\left(y^2\right) }{y^2}\, \operatorname{d}\!y = \frac{1}{2}\int_0^\infty u^{-\frac{3}{2}}{\sin\left(u\right) }\, \operatorname{d}\!x. $$
Now, the last integral is nothing but the Mellin transform of $\sin(x)$ with $s=-\frac{1}{2}$, that is
$$\frac{1}{2}\int_0^\infty u^{-\frac{3}{2}}{\sin\left(u\right) }\, \operatorname{d}\!x= \frac{1}{2}\lim_{s \to -\frac{1}{2} }\Gamma\left( s \right) \sin\left( \frac{\pi s}{2} \right)= \frac{\sqrt {\pi }}{\sqrt{2}},$$
where $\Gamma(s)$ is the gamma function
$$ \Gamma(s)= \int_{0}^{\infty} x^{s-1} e^{-x} dx, \quad Re(s)>0 .$$
Note:
$$ \Gamma\left( -\frac{1}{2} \right) = -2\Gamma\left( \frac{1}{2} \right)=-2 \sqrt{\pi}. $$
$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} &\bbox[5px,#ffd]{\int_{0}^{\infty}\sin\pars{1 \over x^{2}} \,\dd x} \,\,\,\stackrel{x\ =\ t^{-1/4}}{=}\,\,\,\,\,\, {1 \over 4}\int_{0}^{\infty} t^{\color{red}{1/4} - 1}\,\,\, {\sin\pars{\root{t}} \over \root{t}}\,\dd t \end{align} The last integral can be evaluated with Ramanujan's Master Theorem because $\ds{{\sin\pars{\root{t}} \over \root{t}} = \sum_{k = 0}^{\infty} {\pars{-1}^{k} \over \pars{2k + 1}!}\,t^{k} = \sum_{k = 0}^{\infty}\ \color{red}{\Gamma\pars{1 + k} \over \Gamma\pars{2 + 2k}}\,{\pars{-t}^{k} \over k!}}$.
Then, \begin{align} &\bbox[5px,#ffd]{\int_{0}^{\infty}\sin\pars{1 \over x^{2}} \,\dd x} = {1 \over 4}\,\Gamma\pars{\color{red}{1 \over 4}}\, {\Gamma\pars{1 - \color{red}{1/4}} \over \Gamma\pars{2 - 2\bracks{\color{red}{1/4}}}} \\[5mm] = &\ {1 \over 4}\,{\pi \over \sin\pars{\pi/4}}\,{1 \over \pars{1/2}\root{\pi}} = \bbx{{\root{2} \over 2}\root{\pi}} \approx 1.2533 \\ & \end{align}
I prefer to evaluate the more general integral below $$\displaystyle I(a):=\int_{-\infty}^{\infty} \sin \left(\frac{a}{x^2} \right)dx, \tag*{}$$ where $a\geq 0.$
Letting $y=\frac{1}{x^2}$ transforms the integral into
$\displaystyle \begin{aligned} I(a)&=2 \int_{\infty}^0 \sin (a y)\left(-\frac{1}{2 y^{\frac{3}{2}}} d y\right) = \int_0^{\infty} \frac{\sin (a y)}{y^{\frac{3}{2}}} d y \end{aligned} \tag*{} $ Differentiating $I(a)$ w.r.t. $a$, we have $\displaystyle \begin{aligned} I^{\prime}(a) &=\int_0^{\infty} \frac{\cos (a y)}{y^{\frac{1}{2}}} d y\stackrel{u^2=ay}{=}\frac{2}{\sqrt{a}} \int_0^{\infty} \cos u^2 d u \end{aligned} \tag*{} $
Using the result(refer to footnote for details):$ $ $$\displaystyle \int_0^{\infty} \cos x^2 d x=\frac{1}{2}\int_{-\infty}^{\infty} \cos x^2 d x =\sqrt{\frac{\pi}{8}}\tag*{} $$ we obtain $$\displaystyle I^{\prime}(a)=\sqrt{\frac{\pi}{2}} a^{-\frac{1}{2}} \tag*{} $$ Integrating back yields $$\boxed{\displaystyle \int_{-\infty}^{\infty} \sin \left(\frac{a}{x^2} \right)dx=\sqrt{\frac{\pi}{2}} \int_0^a t^{-\frac{1}{2}} d t=\sqrt{2 a \pi}} \tag*{} $$ Putting $a=1$ yields our integral $\boxed{\displaystyle \int_0^{\infty} \sin \left(\frac{1}{x^2} \right)dx=\sqrt{2 \pi}} \tag*{} $
Furthermore, for $a<0$, we have $\displaystyle \int_{-\infty}^{\infty} \sin \left(\frac{a}{x^2} \right)dx= -\sqrt{-2 a\pi}\tag*{}$
Footnote: $\displaystyle \begin{aligned} \int_{-\infty}^{\infty} \cos x^2 d x-i \int_{-\infty}^{\infty} \sin x^2 d x =& \int_{-\infty}^{\infty} e^{-x^2 i} d x \\ =&\frac{\sqrt{2}}{1+i} \int_{-\infty}^{\infty} e^{-\left[\left(\frac{1+i}{\sqrt{2}}\right)x\right]^2} d\left(\frac{1+i}{\sqrt{2}} x\right) \\ =& (1-i)\sqrt{\frac{\pi}{2} } \end{aligned} \tag*{} $ By comparing the real and imaginary parts, we have $\displaystyle \int_{-\infty}^{\infty} \cos x^2 d x=\int_{-\infty}^{\infty} \sin x^2 d x=\sqrt{\frac{\pi}{2}} \tag*{} $
