5

In particular, I am interested in $\xi = z\sqrt{i}$, with $z>0$.

To begin with, formal considerations, such as

$$\begin{align*}\mathcal{L}^{-1}\!\left[F(s)\right]=\frac{1}{2i}\,\mathcal{L}^{-1}\!\left[\frac{e^{i\xi\sqrt{s}}}{\sqrt{s}}\right]-\frac{1}{2i}\,\mathcal{L}^{-1}\!\left[\frac{e^{-i\xi\sqrt{s}}}{\sqrt{s}}\right]=\frac{e^{\frac{1}{4t}(-i\xi)^2}}{2i\,\sqrt{\pi t}}-\frac{e^{\frac{1}{4t}(i\xi)^2}}{2i\,\sqrt{\pi t}}=0,\end{align*}$$

and similar ones all seem to imply $\mathcal{L}^{-1}[F(s)]=0$.

More rigorously, invoking the Bromwich inversion formula

$$\mathcal{L}^{-1}\!\left[F(s)\right] = \int_{\alpha-i\infty}^{\alpha+i\infty}F(s)\,e^{st}ds,$$

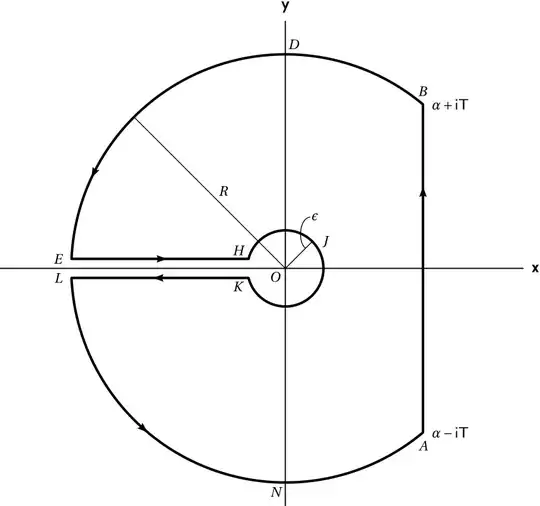
and applying Cauchy's integral theorem to the closed contour depicted below, I obtain

$$\mathcal{L}^{-1}\!\left[F(s)\right] = \lim_{T\to\infty} I_{AB} = - \lim_{\epsilon\to0^+}\big(I_{EH}+I_{KL}\big).$$

The branch cut of $\sqrt{s}$ is taken along the negative real axis. Note as well that the integrals arising from the arcs vanish in the limit $R\to\infty$ by Jordan's Lemma (i.e., considering only $\xi=z\sqrt{i}$, $z>0$). enter image description here However, $$\begin{align*}I_{EH}+I_{KL}&=\int_{-\infty}^0\frac{\sin\big[z\sqrt{i}\,\sqrt{x+i\epsilon}\big]}{\sqrt{x+i\epsilon}}\,e^{xt}+\int_0^{-\infty}\frac{\sin\big[z\sqrt{i}\,\sqrt{x-i\epsilon}\big]}{\sqrt{x-i\epsilon}}\,e^{xt}\\[5pt]&=\int_0^{\infty}\frac{\sin\big[z\sqrt{i}\,\sqrt{i\epsilon-u}\big]}{\sqrt{i\epsilon-u}}\,e^{-ut}-\int_0^{\infty}\frac{\sin\big[z\sqrt{i}\,\sqrt{-u-i\epsilon}\big]}{\sqrt{-u-i\epsilon}}\,e^{-ut}\end{align*},$$ letting $u=-x$ in each integral above. But, $$\int_0^{\infty}\frac{\sin\big[z\sqrt{i}\,\sqrt{\pm i\epsilon-u}\big]}{\sqrt{\pm i\epsilon-u}}\,e^{-ut} = \frac{\sin\big[(-1)^{3/4}z\sqrt{u}\big]}{i\sqrt{u}}\pm\mathcal{O}(\epsilon),$$

consequently

$$\mathcal{L}^{-1}\!\left[F(s)\right] = - \lim_{\epsilon\to0^+}\big(I_{EH}+I_{KL}\big) = 0\qquad :($$

I am expecting $\mathcal{L}^{-1}\!\left[F(s)\right]$ to be a distribution.

Siddhant Das
  • 404
  • Not as a tempered distribution, unless $\xi = 0$. The reason is that either $|e^{i \xi \sqrt s}|$ or $|e^{-i \xi \sqrt s}|$ will grow too fast. Let $z = i \xi \sqrt {\gamma + i \sigma}$. The argument of $z$ approaches a constant value when $\sigma \to \infty$. If $z$ is in the left half-plane, then $-z$ is in the right half-plane. Either $|e^z|$ or $|e^{-z}|$ grows subexponentially unless $\arg \xi = -\pi/4$ or $\arg \xi = 3 \pi/4$. Then either $|e^z|$ or $|e^{-z}|$ still grows subexponentially when $\sigma \to -\infty$. – Maxim Feb 05 '20 at 12:09
  • @Maxim, thanks for your input. In my case $z>0$ and $\xi\propto i^{1/4}$, which is why the Jordan Lemma works out on the bigger arcs as $R\to\infty$. – Siddhant Das Feb 05 '20 at 14:12
  • Rename $z$ in my comment to $\zeta$, it's not related to your $z$. Since the exponentials are unbounded over $\operatorname {Re} s = \gamma$, they're unbounded over the large arcs as well when the radius increases. – Maxim Feb 05 '20 at 14:52

1 Answers1

1

Some elements of reflexion (not an answer as such) in the particular case $\xi=1$ showing there is a problem for Laplace transforms.

1) The infinite product representation of $\sin$ written under the form :

$$\frac{\sin(x)}{x}=\prod_{k=1}^{\infty}(1-\frac{x^2}{k^2\pi^2})\tag{1}$$

gives :

$$\frac{\sin(\sqrt{s})}{\sqrt s}=\prod_{k=1}^{\infty}(1-\frac{s}{k^2\pi^2})\tag{2}$$

which should be Laplace-inverted as a convolution product involving fonctions that cannot have a usual Laplace transform.

Whereas with a Fourier interpretation (with the appropriate variables, in particular with $s$ replaced by $|\nu|$), one would obtain a convolution of inverse Fourier tranforms "tent" functions i.e., squares of cardinal sines, which is meaningful.

2) Another track : $\frac{\sin(\sqrt{s})}{\sqrt s}$ has a simple primitive function : $$-2 \cos(\sqrt{s}) \ \text{(+ constant)}$$ which you don't find on the right hand side of Laplace Transform tables... for the crippling reason that it does not tend to $0$ when $s \to \infty$. Side remark : there is a connection between those two functions (see Difference between sinc and $\cos$ can be expressed using Bessel function $J_{3/2}$) in terms of Bessel functions :

$$\sqrt{\frac 12 \pi \sqrt{s}} J_\frac 32 (\sqrt{s}) = \cfrac{\sin \sqrt{s}}{\sqrt{s}} - \cos \sqrt{s}$$

Jean Marie
  • 81,803