Proving that subgroup of Rotations in $D_{2n}$ is a normal subgroup

Question

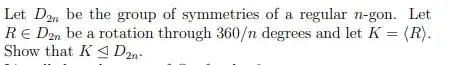
enter image description here

I am trying to prove that the group of rotations in $D_{2n}$ is a normal subgroup.

I know this group has a cardinality $n$, and the ratio of the $D_{2n}$ and $R$ is $2.$

I am trying to construct a homomorphism that sends $<R>$, generator group of rotations to an identity element...

Any clues?

Please do not use pictures for critical portions of your post. Pictures may not be legible, cannot be searched and are not view-able to some, such as those who use screen readers. — Brian61354270, Feb 11 '20 at 16:44
Possible duplicate of Some Subgroup of Dihedral Group is Normal — , Feb 11 '20 at 16:46
thank you very much yes I have seen these posts and i am aware that subgroup of index 2 is normal, i would like to prove it using a homomorphism to kernel.. — gnarm, Feb 11 '20 at 18:37

score 0 · Answer 1 · answered Feb 11 '20 at 17:04

0

Well, as you've noted, $|D_{2n}|/|K|=2$, and so $[D_{2n}:K]=2$ which implies $K$ is normal: see Subgroup of index 2 is Normal.

answered Feb 11 '20 at 17:04

Yuval Gat

1 Answers1