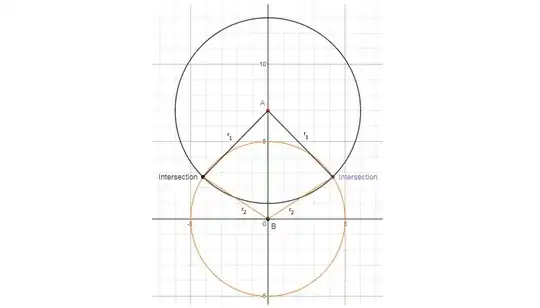
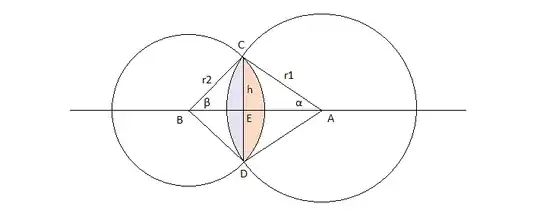
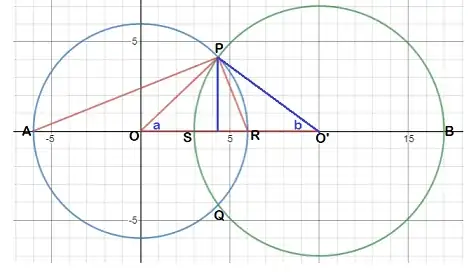
A line segment $\overline{AB}$ has a length of $x$. A circle with center $A$ has a radius of $r_1$, and another circle with center $B$ has a radius of $r_2$. Also, $r_1+r_2>x$ and $x,r_1,r_2>0$ and $r_1,r_2<x$. Is it possible to find the area of the region inside both circles? If so, how?
(example graph of problem(Desmos))
(I don't know if this is a duplicate or not; I will delete this question if it is a duplicate)