I am trying to prove an approximation ratio of an algorithm. I am trying to find an upper bound to $$\frac{\ln\left(\frac{c}{\ln\left(n\right)}\right)}{\ln\left(1-\frac{1}{c}\right)+\frac{1}{c}}$$ where $2\leq c < \ln\left(n\right)$.
Both the numerator and the denominator are negative. The numerator is negative since $\frac{c}{\ln\left(n\right)}<1$ because $c<\ln\left(n\right)$. The denominator is negative since $\ln\left(1-\frac{1}{c}\right)<-\frac{1}{c}$.
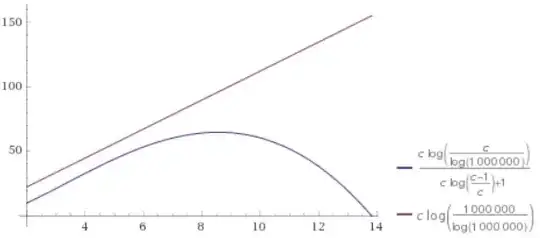
If we set $n$ to be 1e6, the expression looks like:
I tried to use the partial derivative, but I'm failing to isolate $c$: $$\frac{\partial}{\partial c}\left(\frac{\ln\left(\frac{c}{\ln\left(n\right)}\right)}{\ln\left(1-\frac{1}{c}\right)+\frac{1}{c}}\right)=\frac{\left(c-1\right)\left(c\ln\left(1-\frac{1}{c}\right)+1\right)-\ln\left(\frac{c}{\ln\left(n\right)}\right)}{\left(c-1\right)\left(c\ln\left(1-\frac{1}{c}\right)+1\right)^2}$$
Another alternative is to bound the expression by $c\ln\left(\frac{n}{\ln\left(n\right)}\right)$, where $2\leq c < \ln\left(n\right)$: $$\frac{\ln\left(\frac{c}{\ln\left(n\right)}\right)}{\ln\left(1-\frac{1}{c}\right)+\frac{1}{c}}<c\ln\left(\frac{n}{\ln\left(n\right)}\right)$$
I tend to believe that the last inequality is correct based on several examples ($n=1e5$, $n=1e6$, and $n=1e7$). For $n$ equals 1e6: