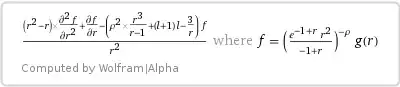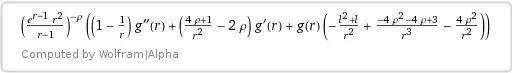How does the author derive these relations?

Question

I am still stuck to the differential equation: $$r(r-1)\partial_r^2f+\partial_rf-\left[ \dfrac{\rho^2r^3}{r-1}+l(l+1)-\dfrac{3}{r} \right]f=0$$

According to the author of this paper, the solution has the form

$$f(r)=(r-1)^\rho r^{-2\rho} \exp(-\rho(r-1))\sum_n a_n\left( \dfrac{r-1}{r} \right)^n.$$

The author susbtitutes this expression into the diff. eqn. and gets a three term recursion relation: $$\alpha_0 a_1+\beta_0 a_0=0$$

$$\alpha_n a_{n+1}+\beta_n a_n+\gamma_n a_{n-1}=0$$

where the coefficients are

$$\alpha_n=n^2+(2+2\rho)n+2\rho+1$$ $$\beta_n=-(n^2+(8\rho+2)n+8\rho^2+4\rho+l(l+1)-3)$$ $$\gamma_n=n^2+4\rho n+4\rho^2 -4$$

What I do not understand is how the author derived these three relations, since substituting $f(r)$ into the diff. eqn. I get a three terms recurrence relation, but with different coefficients.

I use as $\alpha_n$ etc. the coefficients of the powers of $r$: is this correct? Could someone show me the correct derivation?

Answer 1

$\color{brown}{\textbf{Preliminary note.}}$

Equation $$(r^2-r)f''(r) + f'(r) -l(l+1)f(r)= 0\tag1$$ has exact solution $$f(r) = c_1 r^2\operatorname{_2F_1}(1-l, 2+l; 3; r) + c_2 \operatorname {G_{2,\,2}^{2,\,0}} \left(r\big|_{0,\,2}^{1-l,\,2+l}\right),$$ where $\operatorname{_2F_1}(a,b;c;z)$ is the Gauss hypergeometric function and $G$ is the Meijer G-function,

To solve equation $(1)$ can be used Frobenius Metod.

$\color{brown}{\textbf{Substitution.}}$

The author of the paper uses Frobenius method after the substitution $$f(r) = \left(\dfrac{r^2}{r-1}\,e^{r-1}\right)^{-\rho} g(r),\tag2$$ which reduces the polynomials degree.

The given linear homogenius ODE is $$(r^2-r)f''_{rr} + f'_r-\left(\dfrac{\rho^2r^3}{r-1}+l^2+l-\dfrac3r\right)f(r) = 0.\tag3$$

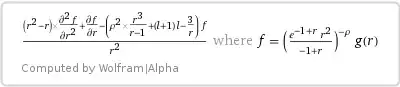
Substiution $(2)$ leads to the equation $$\dfrac{r-1}r (r^2g''_{rr}) + \left(\dfrac{4\rho+1}{r^2}-2\rho\right) (r^2 g'_r) - \left(4\rho^2+l^2+l + \dfrac{4\rho^2+4\rho-3}r\right)g =0.\tag4$$

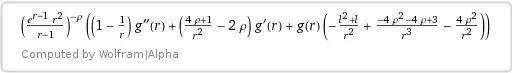
$\color{brown}{\textbf{Frobenius method.}}$

Let $$t=\dfrac{r-1}r,\quad \dfrac1r = 1-t,\quad g(r)=\sum\limits_{n=0}^\infty a_n t^n,\tag5$$ then \begin{align} &\dfrac{4\rho+1}{r^2}-2\rho = (4\rho+1)(1-t)^2-2\rho = 2\rho+1 - (8\rho+2)t + (4\rho+1)t^2,\\[4pt] &4\rho^2+l^2+l + \dfrac{4\rho^2+4\rho-3}r =l^2+l+8\rho^2+4\rho-3 -(4\rho^2+4\rho-3)t,\\[4pt] &t'_r = \dfrac1{r^2} = (1-t)^2,\\[4pt] &r^2g'_r = \dfrac{g'_r}{t'_r} = g'_t = \sum\limits_{n=1}^\infty n a_n t^{n-1},\\[4pt] &g'_r = (1-t)^2g'_t = \sum\limits_{n=1}^\infty n a_n\,t^{n-1} -2\sum\limits_{n=1}^\infty n a_n\,t^n +\sum\limits_{n=1}^\infty na_n\,t^{n+1},\\[4pt] &r^2g''_{rr} = (g'_r)'_t = \sum\limits_{n=1}^\infty n(n-1)a_n\,t^{n-2} -2\sum\limits_{n=1}^\infty n^2a_n\,t^{n-1} +\sum\limits_{n=1}^\infty(n+1)n a_n\,t^n, \end{align}

and from $(4)$ should \begin{align} &\sum\limits_{n=1}^\infty n(n-1)a_n\,t^{n-1} -2\sum\limits_{n=1}^\infty n^2a_n\,t^{n} +\sum\limits_{n=1}^\infty(n+1)n a_n\,t^{n+1}\\ &+(2\rho+1) \sum\limits_{n=1}^\infty n a_n t^{n-1} -(8\rho+2)\sum\limits_{n=1}^\infty n a_n t^{n} + (4\rho+1)\sum\limits_{n=1}^\infty n a_n t^{n+1}\\ & - (l^2+l+8\rho^2+4\rho-3)\sum\limits_{n=0}^\infty a_n t^n +(4\rho^2+4\rho-3)\sum\limits_{n=0}^\infty a_n t^{n+1} =0,\\[4pt] &\sum\limits_{n=1}^\infty(n+1)na_{n+1}\,t^n -2\sum\limits_{n=1}^\infty n^2a_n\,t^n +\sum\limits_{n=1}^\infty n(n-1)a_{n-1}\,t^{n}\\ &+(2\rho+1)a_1+(2\rho+1)\sum\limits_{n=1}^\infty(n+1)a_{n+1}t^{n}\\ &-(8\rho+2)\sum\limits_{n=1}^\infty na_{n}t^{n} + (4\rho+1)\sum\limits_{n=1}^\infty (n-1) a_{n-1} t^{n}\\ &- (l^2+l+8\rho^2+4\rho-3)a_0 - (l^2+l+8\rho^2-4\rho-3)\sum\limits_{n=1}^\infty a_{n} t^{n}\\ & +(4\rho^2+4\rho-3)\sum\limits_{n=1}^\infty a_{n-1} t^{n} = 0,\\[4pt] &(2\rho+1)a_1- (l^2+l+8\rho^2+4\rho-3)a_0\\[4pt] &+\sum\limits_{n=1}^\infty \big((n+1)n+(2\rho+1)(n+1)\big)a_{n+1}\,t^n\\[4pt] &+\sum\limits_{n=1}^\infty \big(-2n^2-(8\rho+2)n-(l^2+l+8\rho^2+4\rho-3)\big)a_n\,t^n\\[4pt] &+\sum\limits_{n=1}^\infty \big(n(n-1)+ (4\rho+1)(n-1)+(4\rho^2+4\rho-3)\big)a_{n-1}\,t^{n}=0,\\[4pt] \end{align} \begin{cases} (2\rho+1)a_1- (l^2+l+8\rho^2+4\rho-3)a_0 = 0,\\[4pt] \big(n^2 + (2\rho+2)n+2\rho+1\big)a_{n+1}\\[4pt] -\big(\color{red}{\mathbf{2}}n^2 +(8\rho+2) n+(l^2+l+8\rho^2+4\rho-3)\big)a_n\\[4pt] +\big(n^2+4\rho n + 4\rho^2-4\big)a_{n-1}=0,\\[4pt] \end{cases} with the single difference in the coefficients from the pointed.