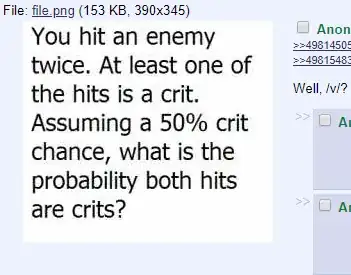
I want to know if the above question can be solved with Bayes' theorem or if they are independent in the same sense that if it rains today it isn't less likely to rain tomorrow. Is the answer 50%, 33.3...%, or something else?
If you want to lose IQ points feel free to see what everyone answered on 4chan.
I don't think this question is the same as this because 25% doesn't seem to be an option for this question at least in my head.