Question:
How to use mathematical induction to show how to tile a $2i \times 3j$ board with $L$ trominoes. The board must be tiled with no squares missing.
Where I am at:
What I don't understand:
How to write the inductive hypothesis and inductive step. I started by defining the base case, then tried to use the principle of divisibility to show any multiple of $2$ or $3$ can be divided by $2$ or $3$ respectfully.
Thanks for your help.
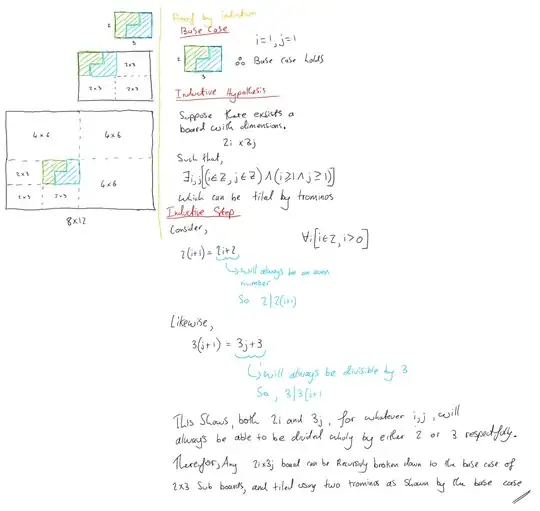
I would say induction is the wrong tool for this proof. You have sketched a nice constructive proof, showing you can tile a $2 \times 3$ rectangle and you can chop a $2i \times 3j$ rectangle into $2 \times 3$ rectangles. Presumably you have been asked to use induction, so here we go.
Note that you have two variables, $i$ and $j$, so you will need two inductions. I will do $j$ first. The base case is that you can tile a $2 \times 3$ rectangle, which you have shown. Then we assume you can tile a $2 \times 3k$ rectangle and show you can tile a $2 \times 3(k+1)$ rectangle. A $2 \times 3(k+1)$ rectangle can be cut into a $2 \times 3k$ rectangle and a $2 \times 3$ rectangle. The first can be tiled by the inductive assumption and the second can be tiled as we have shown. This shows that for all $j$ we can tile a $2 \times 3j$ rectangle.
That result is the base case for the $i$ induction. Now we assume we can tile a $2k \times 3j$ rectangle and want to show we can tile a $2(k+1) \times 3j$ rectangle. Again, we can split the $2(k+1) \times 3j$ rectangle into a $2k \times 3j$ and a $2 \times 3j$ rectangle. The first can be tiled by the inductive assumption and the second can be tiled by the base case. Hence for all $i$ we can tile a $2i \times 3j$ rectangle.
