Here's another solution, if you're open to complex methods.
Substitute $(1)\,u=\sqrt{1-2t^2}$, exploit symmetry, then substitute $(2)\,v=\dfrac{1-u}{1+u}$. This produces two members of a family of integrals that can be evaluated with residue calculus $(3)$.
$$\begin{align*}
\mathcal J &= \int_0^{\tfrac1{\sqrt2}} \frac{\arctan \sqrt{1-2t^2}}{1+t^2} \, dt \\
&= -\sqrt2 \int_0^1 \frac{u \arctan u}{\left(u^2-3\right) \sqrt{1-u^2}} \, du \tag1 \\
&= \frac1{\sqrt2} \int_{-1}^1 \frac{u \arctan u}{\left(u^2-3\right) \sqrt{1-u^2}} \, du \\
&= \frac1{2\sqrt2} \int_0^\infty \left(\sqrt v - \frac1{\sqrt v}\right) \frac{\arctan v - \frac\pi4}{v^2+4v+1} \, dv \tag2 \\
&= \frac1{2\sqrt2} \left[J\left(\frac12\right) - J\left(-\frac12\right)\right] \\
&= \frac\pi4 \lim_{y\to1^-} \arctan \frac{4y^2}{1-y^4} - \frac{\pi^2}{12} = \boxed{\frac{\pi^2}{24}} \tag3
\end{align*}$$
where we denote for non-zero real parameter $-1<a<1$,
$$\bbox[2pt, #fffde7, border: 2px solid red]{J(a) := \int_0^\infty \frac{v^a \arctan v}{v^2+4v+1} \, dv}$$
and notice that
$$\int_0^\infty \frac{\sqrt v-\frac1{\sqrt v}}{v^2+4v+1} \, dv \stackrel{w=\frac1v}= \int_0^\infty \frac{\frac1{\sqrt w}-\sqrt w}{1+4w+w^2} \, dv = 0.$$
To evaluate $J(a)$, consider the integral of
$$f(z) = \frac{z^a \arctan z}{z^2+4z+1} = -\frac i2 \cdot \frac{\lvert z\rvert^a e^{i a \arg z} \left(\log\left\lvert\frac{i-z}{i+z}\right\rvert + i \arg \left(\frac{i-z}{i+z}\right)\right)}{z^2 + 4z + 1}$$
along the positively-oriented triple-keyhole contour $\mathcal C$ (pictured below with the arbitrarily chosen $a=\frac14$, and relocating the poles to make the sketch less cluttered), avoiding branch cuts taken at $[0,\infty)$ and $\pm i [1,\infty)$ so that $\arg z\in(0,2\pi)$ and $\arg\left(\frac{i-z}{i+z}\right)\in(-\pi,\pi)$.
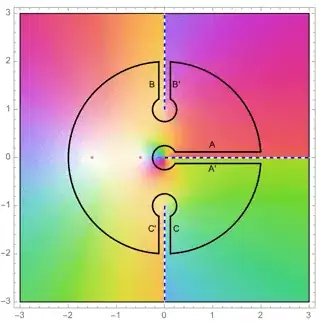
$\mathcal C$ encloses two simple poles at $z=-2\pm\sqrt3$, so by Cauchy's residue theorem,
$$\begin{align*}
\oint_{\mathcal C} f(z) \, dz &= i2\pi \sum \operatorname{Res} f(z) \\
&= \frac{i\pi e^{ia\pi}}{\sqrt3} \left[\left(2+\sqrt3\right)^a \arctan\left(2+\sqrt3\right) - \left(2-\sqrt3\right)^a \arctan\left(2-\sqrt3\right)\right] \\
&= \frac{i\pi^2 e^{ia\pi}}{12\sqrt3} \left(5 \left(2+\sqrt3\right)^a - \left(2-\sqrt3\right)^a\right)
\end{align*}$$
The integrals along the circular portions of $\mathcal C$ will vanish as $R\to\infty$ (large arc's radius) and $\varepsilon\to0^+$ (small arcs' radius). This leaves us with the integrals to either side of each cut which are summarized below.
$$\begin{align*}
\int_A = \int_\varepsilon^R f(x+i\varepsilon) \, dx &\to \int_0^\infty \frac{x^a \arctan x}{x^2 + 4x + 1} \, dx \\
\int_{A'} = \int_R^\varepsilon f(x-i\varepsilon) \, dx &\to -e^{i2a\pi} \int_0^\infty \frac{x^a \arctan x}{x^2+4x+1} \, dx \\
\implies \int_{A\cup A'} &\to \left(1-e^{i2a\pi}\right) J(a) \\[2ex]
\int_B = i \int_{1+\varepsilon}^R f(-\varepsilon+ix) \, dx &\to -\frac12 \int_1^\infty \frac{x^a e^{i\tfrac{a\pi}2} \left(\log\frac{x-1}{x+1} - i \pi\right)}{x^2 - 4ix - 1} \, dx \\
\int_{B'} = i \int_R^{1+\varepsilon} f(\varepsilon+ix) \, dx &\to \frac12 \int_1^\infty \frac{x^a e^{i\tfrac{a\pi}2} \left(\log\frac{x-1}{x+1} + i \pi\right)}{x^2 - 4ix - 1} \, dx \\
\implies \int_{B\cup B'} &\to i\pi e^{i\tfrac{a\pi}2} \int_1^\infty \frac{x^a}{x^2 - 4ix - 1} \, dx \\[2ex]
\int_C = -i \int_{1+\varepsilon}^R f(\varepsilon-ix) \, dx &\to \frac12 \int_1^\infty \frac{x^a e^{i \tfrac{3a\pi}2} \left(\log\frac{x+1}{x-1} + i \pi\right)}{x^2 + 4ix - 1} \, dx \\
\int_{C'} = -i \int_R^{1+\varepsilon} f(-\varepsilon-ix) \, dx &\to -\frac12 \int_1^\infty \frac{x^a e^{i \tfrac{3a\pi}2} \left(\log\frac{x+1}{x-1} - i \pi\right)}{x^2 + 4ix - 1} \, dx \\
\implies \int_{C\cup C'} &\to i\pi e^{i\tfrac{3a\pi}2} \int_1^\infty \frac{x^a}{x^2+4ix-1} \, dx
\end{align*}$$
Totaling up these contributions and solving for $J(a)$ yields
$$\bbox[2pt, #fffde7, border: 2px solid red]{\begin{align*}
J(a) &= \frac{\pi^2\csc(a\pi)}{24\sqrt3} \left(\left(2-\sqrt3\right)^a - 5 \left(2+\sqrt3\right)^a\right) \\
& \qquad \qquad + \frac\pi2 \int_1^\infty \frac{\csc\frac{a\pi}2\,x^2 + 4 \sec\frac{a\pi}2\,x - \csc\frac{a\pi}2\,}{x^4+14x^2+1} \, x^a \, dx
\end{align*}}$$
and thus
$$\begin{align*}
J\left(\frac12\right) &= \frac\pi{\sqrt2} \int_1^\infty \frac{\sqrt x \left(x^2+4x-1\right)}{x^4+14x^2+1} \, dx - \frac{2+\sqrt3}{12\sqrt2} \pi^2 \\
J\left(-\frac12\right) &= -\frac\pi{\sqrt2} \int_1^\infty \frac{x^2-4x-1}{\sqrt x \left(x^4+14x^2+1\right)} \, dx + \frac{2-\sqrt3}{12\sqrt2} \pi^2 \\[2ex]
\implies J\left(\frac12\right) - J\left(-\frac12\right) &= \frac\pi{\sqrt2} \int_1^\infty \frac{x^3+5x^2-5x-1}{\sqrt x \left(x^4+14x^2+1\right)} \, dx - \frac{\pi^2}{3\sqrt2} \\
&\!\!\!\!\!\stackrel{y=\frac{\sqrt x-1}{\sqrt x+1}}= 4\sqrt2\,\pi \int_0^1 \frac{y \left(y^4+1\right)}{y^8 + 14y^4 + 1} \, dy - \frac{\pi^2}{3\sqrt2} \\
&= 2\sqrt2\,\pi \int_0^1 \frac{d\left(y^2-\frac1{y^2}\right)}{\left(y^2 - \frac1{y^2}\right)^2 + 16} - \frac{\pi^2}{3\sqrt2}
\end{align*}$$
