Homology of connected sums

Question

How do you compute the homology groups of $n$ connected sums $H_m(T^2\#T^2\#\dots \#T^2)$ where $T^2$ is the cross product of 2 circles? I know how to compute the homology groups of $T^2$ minus a point and that I need to use the Vietoris-Mayer long exact sequence. But I cannot do it. The computation just gets too messy. Any suggestions? Thank you.

Answer 1

I hope you are familiar with the construction of the torus $T^2$ as the quotient of the square, by identifying edges like this:

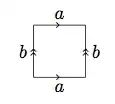
If not, just imagine curving a piece of (stretchy) paper into a cylinder, then bending it so that the two circles meet, and you have a torus.

You should be able to convince yourself that the connected sum operation (cut a disc out of the two spaces and glue the resulting circles together) on tori is the same as cutting a corner off the squares and sticking them together, like this (for $T^2 \# T^2 \# T^2$):

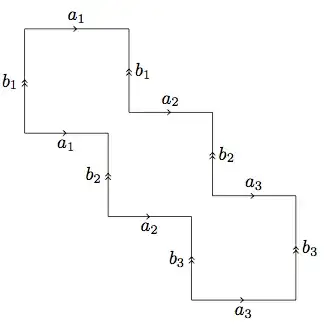
Admittedly, it's a little harder to imagine actually folding this up to get a 3-fold torus, but with sufficiently stretchy material you can do it. If we have an $n$-fold torus (meaning the connected sum of $n$ tori $T^2$), we end up with $4n$ edges, identified in pairs. (This is typically drawn as a regular $4n$-gon, rather than the shape I've given here, but that makes it even harder to see how the quotient works!)

I also hope you know about cellular homology! We've drawn one 0-cell $v$ (all the vertices get identified after you fold up the $4n$-gon), $2n$ 1-cells ($a_1, \dotsc, a_n$ and $b_1, \dotsc, b_n$), and a single 2-cell $F$. The boundary map $\delta_1$ takes any of the 1-cells to $v - v = 0$. The boundary map $\delta_2$ takes $F$ to the sum $a_1 - b_1 + a_2 - b_3 + \dotsb + a_n - b_n - a_n + b_n - \dotsb - a_1 + b_1 = 0$. (You can see in the picture that the boundary of the 2-cell traverses each edge once forwards, and once backwards, so that they cancel out.) If the boundary maps are all 0, then homology is the same as the chain complex, and we have $H_2 = \mathbb{Z}$, $H_1 = \mathbb{Z}^{2n}$, and $H_0 = \mathbb{Z}$ (or replace $\mathbb{Z}$ with the coefficient ring of your choice.)

Answer 2

I'm more familiar with deRahm cohomologies but this argument should work about exactly the same for you. Backwords arrows and trade $\mathbb R$ for $\mathbb Z$ something right? First calculate the cohomology of a punctured 2-manifold torus: $H^kT^2-p$. It's connected so $\dim H^0 T^2-p = 1$ and it's not compact so $H^2 T^2-p \cong \mathbb 0$. Let $U=T^2-p$ and $V$ be a small open ball around $p$ so that $U \cap V$ retracts onto a circle $S^1$. Then $H^kV \cong H^k \mathbb R$ and $H^k(U \cap V) \cong H^k \mathbb S^1$. The sequence is

$$0 \to H^0 T^2 \to H^0 U \oplus H^0 \mathbb R^n \to H^0 S^{n-1} \to H^1 T^2 \to H^1 U \to H^1 S^{n-1} \to H^2 T^2 \to H^2 U \cong 0$$ which in dimensions is just $$ 0=1-2+1-2+\dim H^1U-1+1 $$ or $\dim H^1 U = 2$. You can use that same argument to show that for compact 2-manifold $M$ the cohomology is the same if you puncture it. We can use this in computing the join of tori by induction. The join is connected so the 0th cohomology dimension is 1 and its compact so the 2nd is 1. We need to calculate the 1st. Let $M_n=\#_{i=1}^{n}T^2$. Assume for induction $\dim H^1 M_n=2n$. Then we use a Mayer-Vietoris with $M_{n+1}= A\cup B$ with $A$ the join of n tori with a point missing and $B$ a tori with a point missing so that $A \cap B$ retracts to a circle $S^1$ (as in the definition of the join).

$$0 \to H^0 M_{n+1} \to H^0 A \oplus H^0 B \to H^0 S^{1} \to H^1 M_{n+1} \to H^1 A \oplus H^1 B \to H^1 S^{1} \to H^2 M_{n+1} \to H^2 A \oplus H^2 B \cong 0$$ and that's $$ 0=1-2+1-\dim H^1 M_{n+1}+ 2n+2-1+1 $$ proving the induction.